Question

2．已知F₁、F₂是椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1（a＞b＞0）的左右焦点，P是椭圆上一点，且PF₂⊥F₁F₂，∠PF₁F₂=$\frac{π}{6}$．则椭圆的离心率是（　　）

• A． $\frac{\sqrt{2}}{2}$
• B． $\frac{\sqrt{3}}{3}$
• C． $\frac{1}{2}$
• D． $\frac{\sqrt{5}}{5}$

Answer 1

分析 PF₂⊥F₁F₂，∠PF₁F₂=$\frac{π}{6}$，由勾股定理可知：|PF₁|=2x，|F₁F₂|=$\sqrt{3}$x，由椭圆的定义可知：|PF₁|+|PF₂|=2a，|F₁F₂|=2c，即可求得a和c值，根据椭圆的离心率公式，即可求得椭圆的离心率．

解答 解：由题意可知：椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1（a＞b＞0）焦点在x轴上，|PF₂|=x，
PF₂⊥F₁F₂，∠PF₁F₂=$\frac{π}{6}$，
∴|PF₁|=2x，|F₁F₂|=$\sqrt{3}$x，
又|PF₁|+|PF₂|=2a，|F₁F₂|=2c，
∴2a=3x，2c=$\sqrt{3}$x，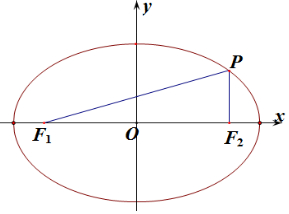

∴C的离心率为：e=$\frac{c}{a}$=$\frac{\sqrt{3}}{3}$．
故选B．

点评 本题考查椭圆的标准方程及简单几何性质，考查勾股定理的应用，考查数形结合思想，属于中档题，