题目内容
4．
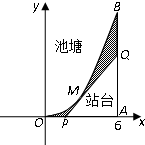如图，池塘的边缘为曲线段OMB，它可以近似看成是函数f（x）=x2在0≤x≤6的图象，BA垂直于x轴于点A，现要建一个以A为直角的观光站台△APQ，其中斜边PQ与曲线段OMB相切于点M（t，t2），切线PQ交x轴于点P，交线段AB于点Q，图中的阴影部分种植草坪．（1）将△QAP的面积表达为t的函数；
（2）求草坪的面积的最小值．
分析 （1）求出函数的导数，求出切线方程，从而求出△QAP的面积；（2）求出函数的导数，解关于导函数的不等式求出函数的极大值即可．
解答 解：（1）f′（x）=2x，所以过点M的切线的斜率为k=f′（t）=2t，…（1分）
由点斜式得切线PQ方程为y-t2=2t（x-t），即y=2tx-t2…①…（2分）
S△QAP=$\frac{1}{2}$|AP|•|AQ|=$\frac{1}{2}$（6-xp）•yQ…②
对①令x=6得yQ=12t-t2…③…（3分）
令y=0，得xp=$\frac{t}{2}$…④…（4分）
③④代入②得S△QAP=$\frac{1}{2}$（6-$\frac{t}{2}$）•（12t-t2）=$\frac{1}{4}$t3-6t2+36t．…（5分）
（2）S′AQAP=$\frac{3}{4}$t2-12t+36，…（6分）
令S′△QAP=0，解得t=4或t=12（舍去）…（7分）
| T | （0，4） | 4 | （4，6） |
| s′ | + | 0 | - |
| s | 增 | 极大值64 | 减 |
所以当t=4时S△QAP有极大值64，
所以当t=4时，△QAP的面积的最大值为64．…（11分）
又${∫}_{0}^{6}$x2dx=72．…（12分）
故草坪的面积的最小值为72-64=8．…（13分）
点评 本题考查了函数的单调性、均值问题，考查导数的应用，是一道中档题．
练习册系列答案
相关题目
19．若函数f（x）=x2+x-lnx+1在其定义域的一个子区间（2k-1，k+2）内不是单调函数，则实数k的取值范围是（ ）
| A． | （-$\frac{3}{2}$，$\frac{3}{4}$） | B． | [$\frac{1}{2}$，3） | C． | （-$\frac{3}{2}$，3） | D． | [$\frac{1}{2}$，$\frac{3}{4}$） |