题目内容
若把直线l：2x+y-2=0向右平移2个单位，再向下平移1个单位，所得直线的方程是（ ）
| A、2x+y-5=0 |
| B、2x-y-5=0 |
| C、2x-y+5=0 |
| D、2x+y+5=0 |
考点：函数的图象与图象变化
专题：函数的性质及应用
分析：根据“上加下减，左加右减”化简即可
解答：
解：∵2x+y-2=0，
∴y=-2x+2，
∵向右平移2个单位，再向下平移1个单位，
∴y=-2（x-2）+2-1=-2x+5，
即2x+y-5=0
故选：A．
∴y=-2x+2，
∵向右平移2个单位，再向下平移1个单位，
∴y=-2（x-2）+2-1=-2x+5，
即2x+y-5=0
故选：A．
点评：本题考查了一次函数的图象的平移，属于基础题
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
函数y=x2+bx+c（x∈[0，∞））是单调函数的充要条件是（ ）
| A、b≥0 | B、b＞0 |
| C、b＜0 | D、b≤0 |
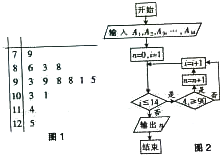如图是某高三学生14次数学考试成绩的茎叶图（图1），现在将该14个数据依次记为A1，A2，…，A14，并输入如图2所示的一个算法流程图，那么该算法流程图运行结束时输出n的值是（ ）| A、10 | B、9 | C、8 | D、7 |
定义运算：
=a1a4-a2a3，若将函数f（x）=
的图象向左平移m（m＞0）的单位后，所得图象对于的函数为偶函数，则m的最小值是（ ）
|
|
A、
| ||
B、
| ||
C、
| ||
D、
|
角θ的顶点为坐标原点，始边与x轴的非负半轴重合，终边在直线y=2x上，则cos2θ=（ ）
A、-
| ||
B、
| ||
C、-
| ||
D、
|
