题目内容
定义运算:
=a1a4-a2a3,若将函数f(x)=
的图象向左平移m(m>0)的单位后,所得图象对于的函数为偶函数,则m的最小值是( )
|
|
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:函数y=Asin(ωx+φ)的图象变换,两角和与差的正弦函数
专题:三角函数的图像与性质
分析:先用行列式展开法则求出f(x),再由函数的平移公式能够得到f(x+m),然后由偶函数的性质求出m的最小值.
解答:
解:f(x)=
=
sinx-cosx=2sin(x-
),
图象向左平移m(m>0)个单位,
得f(x+m)=2sin(x+m-
),
由m-
=
+kπ,k∈Z,
则当m取得最小值
时,函数为偶函数.
故选:C.
|
| 3 |
| π |
| 6 |
图象向左平移m(m>0)个单位,
得f(x+m)=2sin(x+m-
| π |
| 6 |
由m-
| π |
| 6 |
| π |
| 2 |
则当m取得最小值
| 2π |
| 3 |
故选:C.
点评:本题考查二阶行列式的展开法则、函数的图象与图象变化,解题时要注意函数的平移和偶函数的合理运用,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
给定两个命题p,q,若¬p是q的必要而不充分条件,则p是¬q的( )
| A、必要而不充分条件 |
| B、充分而不必要条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
已知数列{an}的前n项和Sn满足SnS1=Sn+1(n∈N*),且a1=2,那么a7=( )
| A、128 | B、16 | C、32 | D、64 |
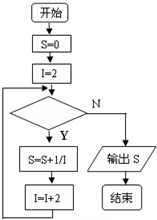
如图给出的是计算
+
+
+…+
的值的一个程序框图,其中判断框内应填入的条件是( )
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 6 |
| 1 |
| 100 |

| A、i≤100 | B、i>100 |
| C、i>50 | D、i≤50 |
若把直线l:2x+y-2=0向右平移2个单位,再向下平移1个单位,所得直线的方程是( )
| A、2x+y-5=0 |
| B、2x-y-5=0 |
| C、2x-y+5=0 |
| D、2x+y+5=0 |
已知直线l:y=3x-2的纵截距是( )
| A、-3 | B、-2 | C、3 | D、2 |
如图是一个体积为4的空间几何体的三视图,则图中x的值为( )
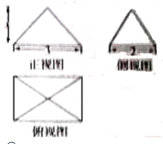

| A、2 | B、3 | C、4 | D、5 |