题目内容
已知在平面直角坐标系xoy中，直线AB的方程为3x-2y+6=0，直线AC的方程为2x+3y-22=0，直线BC的方程为3x+4y-m=0．
（1）求证：△ABC为直角三角形；
（2）当△ABC的BC边上的高为1时，求m的值．
（1）求证：△ABC为直角三角形；
（2）当△ABC的BC边上的高为1时，求m的值．
考点：直线的一般式方程与直线的垂直关系
专题：直线与圆
分析：（1）由两直线方程得到两直线的斜率，由斜率之积等于-1得到直线AB与AC互相垂直，从而说明△ABC为直角三角形；
（2）联立方程组求得A的坐标，然后由A到BC边的距离为1求得m的值．
（2）联立方程组求得A的坐标，然后由A到BC边的距离为1求得m的值．
解答：
解：（1）直线AB的斜率为kAB=
，
直线AC的斜率为kAC=-
，
∵kAB•kAC=-1，
∴直线AB与AC互相垂直，
因此，△ABC为直角三角形；
（2）解方程组
，得
，即A（2，6），
设点A到直线BC的距离为d，则d=
=
，
依题意有d=1，即
=1，即|30-m|=5，解得m=25或35．
| 3 |
| 2 |
直线AC的斜率为kAC=-
| 2 |
| 3 |
∵kAB•kAC=-1，
∴直线AB与AC互相垂直，
因此，△ABC为直角三角形；
（2）解方程组
|
|
设点A到直线BC的距离为d，则d=
| |3×2+4×6-m| | ||
|
| |30-m| |
| 5 |
依题意有d=1，即
| |30-m| |
| 5 |
点评：本题考查了直线的一般式方程与直线垂直的关系，考查了点到直线距离公式的应用，是基础题．
练习册系列答案
阅读快车系列答案
相关题目
若把直线l：2x+y-2=0向右平移2个单位，再向下平移1个单位，所得直线的方程是（ ）
| A、2x+y-5=0 |
| B、2x-y-5=0 |
| C、2x-y+5=0 |
| D、2x+y+5=0 |
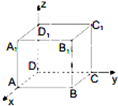如图，把棱长为2的正方体ABCD-A1B1C1D1放在空间直角坐标系中，使D与原点重合，点A与点C分别放在x轴和y轴的正半轴上，则B1的坐标为：（ ）| A、（2，2，2） |
| B、（2，2，0） |
| C、（2，0，2） |
| D、（0，2，2） |
如图所示曲线是幂函数y=xa在第一象限内的图象，其中a=±| 1 |
| 2 |
A、
| ||||
B、2、
| ||||
C、-
| ||||
D、2、
|