题目内容
已知f（x）是定义在R上的奇函数，当x＞0时，f（x）=
，则f（-4）= ．
| x |
考点：函数奇偶性的性质
专题：函数的性质及应用
分析：将x＞0的解析式中的x用4代替，求出f（4），利用奇函数的定义得到f（-4）与f（4）的关系，即可求出f（-4）．
解答：
解：解：∵当x＞0时，f（x）=
，
∴f（4）=2，
∵f（x）是定义在R上的奇函数，
∴f（-4）=-f（4），
∴f（-4）=-2．
故答案为：-2．
| x |
∴f（4）=2，
∵f（x）是定义在R上的奇函数，
∴f（-4）=-f（4），
∴f（-4）=-2．
故答案为：-2．
点评：本题考查的知识点是函数奇偶性的性质，熟练掌握函数的奇偶性的性质是解答本题的关键．属于基础题．
练习册系列答案
相关题目
若把直线l：2x+y-2=0向右平移2个单位，再向下平移1个单位，所得直线的方程是（ ）
| A、2x+y-5=0 |
| B、2x-y-5=0 |
| C、2x-y+5=0 |
| D、2x+y+5=0 |
如图是一个体积为4的空间几何体的三视图，则图中x的值为（ ）
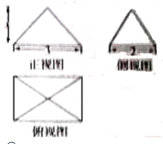
| A、2 | B、3 | C、4 | D、5 |
已知a，b为正数，且满足2＜a+2b＜4，那么3a-b的取值范围是（ ）
| A、（-4，6） |
| B、（-2，6） |
| C、（-4，12） |
| D、（-2，12） |
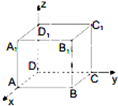如图，把棱长为2的正方体ABCD-A1B1C1D1放在空间直角坐标系中，使D与原点重合，点A与点C分别放在x轴和y轴的正半轴上，则B1的坐标为：（ ）| A、（2，2，2） |
| B、（2，2，0） |
| C、（2，0，2） |
| D、（0，2，2） |