题目内容
9.设O为坐标原点,已知椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,抛物线C2:x2=-ay的准线方程为y=$\frac{1}{2}$.(1)求椭圆C1和抛物线C2的方程;
(2)设过定点M(0,2)的直线t与椭圆C1交于不同的两点P,Q,若O在以PQ为直径的圆的外部,求直线t的斜率k的取值范围.
分析 (1)根据准线方程计算a,利用离心率计算c,从而得出b;
(2)设直线t的斜率为k,得出直线t的方程,联立方程组消元,根据根与系数的关系计算$\overrightarrow{OP}•\overrightarrow{OQ}$,令$\overrightarrow{OP}•\overrightarrow{OQ}$>0得出k的范围.
解答 解:(1)∵抛物线C2:x2=-ay的准线方程为y=$\frac{1}{2}$,
∴$\frac{a}{4}=\frac{1}{2}$,解得a=2
∴抛物线C2的方程为x2=-2y,
∵椭圆C1的离心率e=$\frac{c}{a}$=$\frac{\sqrt{3}}{2}$,∴c=$\sqrt{3}$,
∴b2=a2-c2=1,
∴椭圆C1的方程为$\frac{{x}^{2}}{4}+{y}^{2}$=1.
(2)当直线t无斜率时,O为PQ的中点,不符合题意;
当直线t有斜率时,设直线t的方程为y=kx+2,
联立方程组$\left\{\begin{array}{l}{\frac{{x}^{2}}{4}+{y}^{2}=1}\\{y=kx+2}\end{array}\right.$,消元得:(1+4k2)x2+16kx+12=0.
∵直线t与椭圆交于两点,
∴△=256k2-48(1+4k2)>0,∴k<-$\frac{\sqrt{3}}{2}$或k>$\frac{\sqrt{3}}{2}$,
设P(x1,y1),Q(x2,y2),则x1+x2=$\frac{-16k}{1+4{k}^{2}}$,x1x2=$\frac{12}{1+4{k}^{2}}$,
∴y1y2=(kx1+2)(kx2+2)=k2x1x2+2k(x1+x2)+4,
∴$\overrightarrow{OP}•\overrightarrow{OQ}$=x1x2+y1y2=$\frac{12(1+{k}^{2})}{1+4{k}^{2}}$-$\frac{32{k}^{2}}{1+4{k}^{2}}$+4=$\frac{16-4{k}^{2}}{1+4{k}^{2}}$.
∵O在以PQ为直径的圆的外部,∴∠POQ∈(0,$\frac{π}{2}$),∴$\overrightarrow{OP}•\overrightarrow{OQ}$>0,
∴16-4k2>0,解得-2<k<2.
综上,k的取值范围是(-2,-$\frac{\sqrt{3}}{2}$)∪($\frac{\sqrt{3}}{2}$,2).
点评 本题考查了圆锥曲线的性质,直线与圆锥曲线的位置关系,常利用根与系数的关系化简计算,属于中档题.

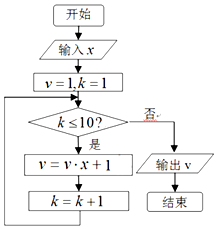 秦九韶是我国南宋时期的数学家,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法,如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例,若输入x的值为 2,则输出v的值为( )
秦九韶是我国南宋时期的数学家,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法,如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例,若输入x的值为 2,则输出v的值为( )| A. | 211-1 | B. | 211-2 | C. | 210-1 | D. | 210-2 |
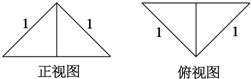 把边长为1的正方形ABCD沿对角线BD折起,形成的三棱锥A-BCD的正视图与俯视图如图所示,则其侧视图的面积为$\frac{1}{4}$,二面角B-AC-D的余弦值为$-\frac{1}{3}$.
把边长为1的正方形ABCD沿对角线BD折起,形成的三棱锥A-BCD的正视图与俯视图如图所示,则其侧视图的面积为$\frac{1}{4}$,二面角B-AC-D的余弦值为$-\frac{1}{3}$. | A. | 合情推理 | B. | 演绎推理 | C. | 类比推理 | D. | 归纳推理 |
| A. | 2∈A | B. | 2∉A | C. | 2>A | D. | 2?A |