题目内容
7.已知命题甲是“{x|$\frac{{x}^{2}+x}{x-1}$≥0}”,命题乙是“{x|log3(2x+1)≤0}”,则甲是乙的必要不充分条件.(从充分不必要、必要不充分、充要、既不充分也不必要中选填)分析 利用不等式的解法分别化简甲乙命题,进而判断出结论.
解答 解:命题甲:$\frac{{x}^{2}+x}{x-1}$≥0,化为x(x-1)(x+1)≥0,且x≠1,解得:-1≤x≤0,或x>1.
命题乙:log3(2x+1)≤0,化为0<2x+1≤1,解得:$-\frac{1}{2}<x≤$0.
则甲是乙的必要不充分条件.
故答案为:必要不充分.
点评 本题考查了不等式的解法、简易逻辑的判定方法,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
2.华为推出一款6寸大屏手机,现对500名该手机使用者(200名女性,300名男性)进行调查,对手机进行打分,打分的频数分布表如下:
女性用户:
男性用户:
(1)如果评分不低于70分,就表示该用户对手机“认可”,否则就表示“不认可”,完成下列2×2列联表,并回答是否有95%的把握认为性别对手机的“认可”有关:
附:
K2=$\frac{n(a+d-b+c)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
(2)根据评分的不同,运动分层抽样从男性用户中抽取20名用户,在这20名用户中,从评分不低于80
分的用户中任意抽取3名用户,求3名用户中评分小于90分的人数的分布列和数学期望.
女性用户:
| 分值区间 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100) |
| 频数 | 20 | 40 | 80 | 50 | 10 |
| 分值区间 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100) |
| 频数 | 45 | 75 | 90 | 60 | 30 |
| 女性用户 | 男性用户 | 合计 | |
| “认可”手机 | 140 | 180 | 320 |
| “不认可”手机 | 60 | 120 | 180 |
| 合计 | 200 | 300 | 500 |
| P(K2≧k) | 0.05 | 0.01 |
| k | 3.841 | 6.635 |
(2)根据评分的不同,运动分层抽样从男性用户中抽取20名用户,在这20名用户中,从评分不低于80
分的用户中任意抽取3名用户,求3名用户中评分小于90分的人数的分布列和数学期望.
19.已知x,y的取值如表:
若x,y具有线性相关关系,且回归方程为$\hat y=0.95x+2.6$,则a=2.2.
| x | 0 | 1 | 3 | 4 |
| y | a | 4.3 | 4.8 | 6.7 |
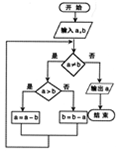 如图程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若输入的a,b分别为17,14,则输出的a=( )
如图程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若输入的a,b分别为17,14,则输出的a=( )