题目内容
4.已知函数f(x)=lnx+bx-c,f(x)在点(1,f(1))处的切线方程为x+y+4=0.(1)求f(x)的解析式;
(2)求f(x)的单调区间;
(3)若函数f(x)在定义域内恒有f(x)≥2lnx+kx成立,求k的取值范围.
分析 (1)求出函数的导数,计算f(1),f′(1),结合切线方程求出b,c的值,从而求出函数f(x)的解析式即可;
(2)求出函数f(x)的导数,解关于导函数的不等式,求出函数的单调区间即可;
(3)问题转化为$k≤-2-\frac{lnx+3}{x}$在定义域(0,+∞)内恒成立,设$g(x)=-2-\frac{lnx+3}{x}$,根据函数的单调性求出k的范围即可.
解答 解:(1)由题意,得$f'(x)=\frac{1}{x}+b$,
则f'(1)=1+b,∵在点(1,f(1))处的切线方程为x+y+4=0,
∴切线斜率为-1,则1+b=-1,得b=-2,
将(1,f(1))代入方程x+y+4=0,得1+f(1)+4=0,解得f(1)=-5,
∴f(1)=b-c=-5,将b=-2代入得c=3,
故f(x)=lnx-2x-3.
(2)依题意知函数的定义域是(0,+∞),且$f'(x)=\frac{1}{x}-2$,
令f'(x)>0,得$0<x<\frac{1}{2}$,令f'(x)<0,得$x>\frac{1}{2}$,
故f(x)的单调增区间为$(0,\frac{1}{2})$,单调减区间为$(\frac{1}{2},+∞)$.
(3)由f(x)≥2lnx+kx,得lnx-2x-3≥2lnx+kx,
∴$k≤-2-\frac{lnx+3}{x}$在定义域(0,+∞)内恒成立.
设$g(x)=-2-\frac{lnx+3}{x}$,则$g'(x)=\frac{lnx+2}{x^2}$,
令g'(x)=0,得x=e-2.
令g'(x)>0,得x>e-2,令g'(x)<0,得0<x<e-2,
故g(x)在定义域内有极小值g(e-2),此极小值又为最小值.
∴g(x)的最小值为$g({e^{-2}})=-2-\frac{{ln{e^{-2}}+3}}{{{e^{-2}}}}=-2-{e^2}$,
所以k≤-2-e2,即k的取值范围为(-∞,-2-e2].
点评 本题考查了切线方程问题,考查函数的单调性、最值问题,考查导数的应用以及函数恒成立问题,是一道综合题.

| x | 0 | 1 | 3 | 4 |
| y | a | 4.3 | 4.8 | 6.7 |
| A. | f(x)=x2+1,x∈[-2,2) | B. | f(x)=|3x-1|-|3x+1| | ||
| C. | f(x)=-x2+1,x∈(-2,+∞) | D. | f(x)=x4 |
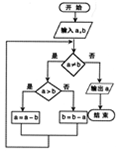 如图程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若输入的a,b分别为17,14,则输出的a=( )
如图程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若输入的a,b分别为17,14,则输出的a=( )
 如图,已知六棱锥P-ABCDEF的底面是正六边形,PA⊥平面ABC,PA=2AB,则下列结论正确的是④( 写出所以正确结论的序号)
如图,已知六棱锥P-ABCDEF的底面是正六边形,PA⊥平面ABC,PA=2AB,则下列结论正确的是④( 写出所以正确结论的序号)