题目内容
18.已知F1(-4,0),F2(4,0)为椭圆$\frac{x^2}{25}+\frac{y^2}{9}=1$的两个焦点,P在椭圆上,且△PF1F2的面积为$3\sqrt{3}$,则cos∠F1PF2=$\frac{1}{2}$.分析 由已知条件利用椭圆定义和余弦定理列出方程组,再由三角形面积利用正弦定理求出1-cosθ=$\sqrt{3}$sinθ,由此利用sin2θ+cos2θ=1,能求出cosθ.
解答 解:∵F1(-4,0),F2(4,0)为椭圆$\frac{x^2}{25}+\frac{y^2}{9}=1$的两个焦点,
P在椭圆上,且△PF1F2的面积为$3\sqrt{3}$,设|PF1|=m,|PF2|=n,
∴$\left\{\begin{array}{l}{{m}^{2}+{n}^{2}+2mn=100}\\{{m}^{2}+{n}^{2}=2mncos∠{F}_{1}P{F}_{2}=64}\end{array}\right.$,
整理,得mn=$\frac{18}{1-cos∠{F}_{1}P{F}_{2}}$,
∵△PF1F2的面积为3$\sqrt{3}$,
∴$\frac{1}{2}$×$\frac{18}{1-cos∠{F}_{1}P{F}_{2}}$×sin∠F1PF2=3$\sqrt{3}$,
∴1-cos∠F1PF2=$\sqrt{3}$sin∠F1PF2,
∵sin2∠F1PF2+cos2∠F1PF2=1,∴cos∠F1PF2=$\frac{1}{2}$.
故答案为:$\frac{1}{2}$
点评 本题考查角的余弦值的求法,是中档题,解题时要认真审题,注意椭圆性质、余弦定理的合理运用.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
7.下列函数中是偶函数的是( )
| A. | f(x)=x2+1,x∈[-2,2) | B. | f(x)=|3x-1|-|3x+1| | ||
| C. | f(x)=-x2+1,x∈(-2,+∞) | D. | f(x)=x4 |
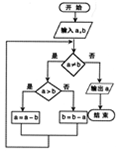 如图程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若输入的a,b分别为17,14,则输出的a=( )
如图程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若输入的a,b分别为17,14,则输出的a=( ) 如图,已知六棱锥P-ABCDEF的底面是正六边形,PA⊥平面ABC,PA=2AB,则下列结论正确的是④( 写出所以正确结论的序号)
如图,已知六棱锥P-ABCDEF的底面是正六边形,PA⊥平面ABC,PA=2AB,则下列结论正确的是④( 写出所以正确结论的序号) 如图,在正方体ABCD-A1B1C1D1中,E是CC1的中点,求证:
如图,在正方体ABCD-A1B1C1D1中,E是CC1的中点,求证: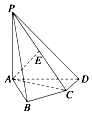 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中点.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中点.