题目内容
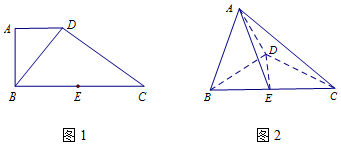
4.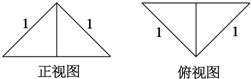 把边长为1的正方形ABCD沿对角线BD折起,形成的三棱锥A-BCD的正视图与俯视图如图所示,则其侧视图的面积为$\frac{1}{4}$,二面角B-AC-D的余弦值为$-\frac{1}{3}$.
把边长为1的正方形ABCD沿对角线BD折起,形成的三棱锥A-BCD的正视图与俯视图如图所示,则其侧视图的面积为$\frac{1}{4}$,二面角B-AC-D的余弦值为$-\frac{1}{3}$.
分析 由题意画出图形,得到几何体侧视图的形状,求出三角形边长,代入三角形面积公式求得侧视图的面积;再找出二面角B-AC-D的平面角,求解三角形可得二面角B-AC-D的余弦值.
解答 解:由三视图可得原几何体如图,
该三棱锥的侧面ABD与底面CBD是全等的等腰直角三角形,且平面ABD⊥底面CBD,
过A作AO⊥BD,垂足为O,连接CO,则侧视图为等腰直角三角形AOC,
∵AO=OC=$\frac{\sqrt{2}}{2}$,∴${S}_{△AOC}=\frac{1}{2}×\frac{\sqrt{2}}{2}×\frac{\sqrt{2}}{2}=\frac{1}{4}$;
取AC的中点G,连接BG,DG,则∠BGD为二面角B-AC-D的平面角.
∵△ADC、△ABC是边长为1的正三角形,∴$BG=DG=\frac{\sqrt{3}}{2}$,
在△BGD中,由余弦定理可得:cos∠BGD=$\frac{(\frac{\sqrt{3}}{2})^{2}+(\frac{\sqrt{3}}{2})^{2}-(\sqrt{2})^{2}}{2×\frac{\sqrt{3}}{2}×\frac{\sqrt{3}}{2}}$=-$\frac{1}{3}$.
故答案为:$\frac{1}{4},-\frac{1}{3}$.
点评 本题考查二面角的平面角的求法,考查空间想象能力和思维能力,训练了余弦定理在求解三角形中的应用,是中档题.

练习册系列答案
 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
2.华为推出一款6寸大屏手机,现对500名该手机使用者(200名女性,300名男性)进行调查,对手机进行打分,打分的频数分布表如下:
女性用户:
男性用户:
(1)如果评分不低于70分,就表示该用户对手机“认可”,否则就表示“不认可”,完成下列2×2列联表,并回答是否有95%的把握认为性别对手机的“认可”有关:
附:
K2=$\frac{n(a+d-b+c)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
(2)根据评分的不同,运动分层抽样从男性用户中抽取20名用户,在这20名用户中,从评分不低于80
分的用户中任意抽取3名用户,求3名用户中评分小于90分的人数的分布列和数学期望.
女性用户:
| 分值区间 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100) |
| 频数 | 20 | 40 | 80 | 50 | 10 |
| 分值区间 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100) |
| 频数 | 45 | 75 | 90 | 60 | 30 |
| 女性用户 | 男性用户 | 合计 | |
| “认可”手机 | 140 | 180 | 320 |
| “不认可”手机 | 60 | 120 | 180 |
| 合计 | 200 | 300 | 500 |
| P(K2≧k) | 0.05 | 0.01 |
| k | 3.841 | 6.635 |
(2)根据评分的不同,运动分层抽样从男性用户中抽取20名用户,在这20名用户中,从评分不低于80
分的用户中任意抽取3名用户,求3名用户中评分小于90分的人数的分布列和数学期望.
19.已知x,y的取值如表:
若x,y具有线性相关关系,且回归方程为$\hat y=0.95x+2.6$,则a=2.2.
| x | 0 | 1 | 3 | 4 |
| y | a | 4.3 | 4.8 | 6.7 |
16.已知O是坐标原点,点A(1,0),若点M(x,y)为平面区域$\left\{\begin{array}{l}{x+y≥2}\\{x≤1}\\{y≤2}\end{array}\right.$上的一个动点,则|$\overrightarrow{OA}$+$\overrightarrow{OM}$|的取值范围是( )
| A. | [$\sqrt{5}$,2$\sqrt{2}$] | B. | [$\frac{1}{2}$,1] | C. | [$\frac{3\sqrt{2}}{2}$,2$\sqrt{2}$] | D. | [$\frac{\sqrt{2}}{2}$,$\sqrt{2}$] |