题目内容
12．判断函数 f（x）=x2 在R上的增减性．分析 首先，确定函数奇偶性，然后，利用单调性的定义，进行区间判断即可．
解答 解：因为f（x）=x2 为偶函数，
当x∈（0，+∞）时，设x1＜x2∈（0，+∞），
∴f（x1）-f（x2）=x12-x22=（x1-x2）（x1+x2），
∵x1＜x2∈（0，+∞），
∴x1-x2＜0，x1+x2＞0，
∴f（x1）-f（x2）＜0，
∴f（x1）＜f（x2），
∴f（x）在（0，+∞）上为增函数，
∴f（x）在（-∞，0]上为减函数．
点评 本题主要考查函数单调性定义，和函数的奇偶性，属于基础题．
练习册系列答案
相关题目
2．等比数列{an}前四项和为1，前8项和为17，则它的公比为（ ）
| A． | 2 | B． | -2 | C． | 2或-2 | D． | 2或-1 |
20．已知数列{an}中，${a_1}=\frac{3}{4}$，${a_n}=1-\frac{1}{{{a_{n-1}}}}$（n≥2），则a2016=（ ）
| A． | $\frac{3}{4}$ | B． | $-\frac{1}{3}$ | C． | $-\frac{3}{4}$ | D． | 4 |
7．
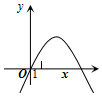已知二次函数y=ax2+bx+c=0（a≠0）的图象如图所示，记p=|a-b+c|+|2a+b|，q=|a+b+c|+|2a-b|，则（ ）
已知二次函数y=ax2+bx+c=0（a≠0）的图象如图所示，记p=|a-b+c|+|2a+b|，q=|a+b+c|+|2a-b|，则（ ）| A． | p＞q | B． | p=q | ||
| C． | p＜q | D． | p，q大小关系不能确定 |