题目内容
20.已知数列{an}中,${a_1}=\frac{3}{4}$,${a_n}=1-\frac{1}{{{a_{n-1}}}}$(n≥2),则a2016=( )| A. | $\frac{3}{4}$ | B. | $-\frac{1}{3}$ | C. | $-\frac{3}{4}$ | D. | 4 |
分析 由递推公式先依次求出数列的前4项,从而得到数列{an}是以3为周期的周期数列,由此能求出a2016.
解答 解:∵数列{an}中,${a_1}=\frac{3}{4}$,${a_n}=1-\frac{1}{{{a_{n-1}}}}$(n≥2),
∴a2=1-$\frac{1}{\frac{3}{4}}$=-$\frac{1}{3}$,
${a}_{3}=1-\frac{1}{-\frac{1}{3}}$=4,
${a}_{4}=1-\frac{1}{4}$=$\frac{3}{4}$,
∴数列{an}是以3为周期的周期数列,
∴a2016=a3=4.
故选:D.
点评 本题考查数列的第2016项的求法,是基础题,解题时要认真审题,注意递推思想的合理运用.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
10.下列函数是奇函数的是( )
| A. | f(x)=log2x | B. | f(x)=x2 | C. | f(x)=3x | D. | f(x)=x3 |
15.已知命题P:函数y=sin$\frac{π}{2}$x在x=a处取到最大值;命题q:直线x-y+2=0与圆(x-3)2+(y-a)2=8相切;则p是q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
5.函数y=ax2+bx+3在(-∞,-1]上是增函数,在[-1,+∞)上是减函数,则( )
| A. | b>0且a<0 | B. | b=2a<0 | C. | b=2a>0 | D. | b=-2a<0 |
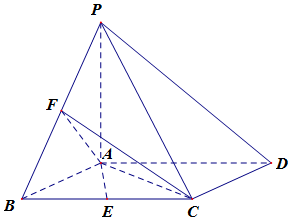 如图所示,已知四棱锥P-ABCD中,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E,F分别是BC,PB的中点.
如图所示,已知四棱锥P-ABCD中,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E,F分别是BC,PB的中点.