题目内容
某厂生产某种产品x件的总成本c(x)=1200+
x3(万元),已知产品单价的平方与产品件数x成反比,生产100件这样的产品单价为50万元,则产量定为 件时,总利润最大.
| 2 |
| 75 |
考点:函数最值的应用
专题:计算题,应用题,函数的性质及应用,导数的综合应用
分析:分析题目数据建立数学模型,得出总利润函数L(x)=
•x-(1200+
x3)(x>0),注意定义域,然后利用导数求其最值,还原为实际问题即可.
| 500 | ||
|
| 2 |
| 75 |
解答:
解:设产品单价为p,则有p2=
,
将x=100,p=50代入,得k=250000,
所以p=p(x)=
,
设总利润为L,L=L(x)=p(x)-c(x)=
•x-(1200+
x3)(x>0)
即L(x)=
•x-1200-
x3,L'(x)=
-
,
令L'(x)=0,即
-
=0,解得x=25,
因为x=25是函数L(x)在(0,+∞)上唯一的极值点,
且是极大值点,从而是最大值点.
故答案为:25.
| k |
| x |
将x=100,p=50代入,得k=250000,
所以p=p(x)=
| 500 | ||
|
设总利润为L,L=L(x)=p(x)-c(x)=
| 500 | ||
|
| 2 |
| 75 |
即L(x)=
| 500 | ||
|
| 2 |
| 75 |
| 250 | ||
|
| 2x2 |
| 25 |
令L'(x)=0,即
| 250 | ||
|
| 2x2 |
| 25 |
因为x=25是函数L(x)在(0,+∞)上唯一的极值点,
且是极大值点,从而是最大值点.
故答案为:25.
点评:本题考查利用导数解决生活中的优化问题的方法和步骤,属于中档题.

练习册系列答案
相关题目
若函数f(x)=logax(a>0且a≠0)在[4,16]上的最大值比最小值大1,则实数a的值为( )
A、
| ||
B、
| ||
| C、4 | ||
| D、以上都不对 |
给出如图的程序框图,那么输出的数是( )


| A、3 | B、4 | C、5 | D、6 |
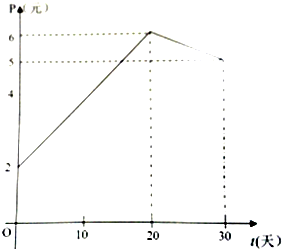 已知某上市股票在30天内每股的交易价格P(元)与时间t(天)组成有序数对(t,p),点(t,p)落在图中的两条线段上,该股票在30天内(包括30天)的日交易量Q(万股)与时间t(天)的部分数据如下表所示
已知某上市股票在30天内每股的交易价格P(元)与时间t(天)组成有序数对(t,p),点(t,p)落在图中的两条线段上,该股票在30天内(包括30天)的日交易量Q(万股)与时间t(天)的部分数据如下表所示