题目内容
(1)已知椭圆的一个焦点坐标为(4,0),离心率为
,求椭圆的标准方程;
(2)已知双曲线的渐近线方程为y=±
x,准线方程为x=±
,求该双曲线的标准方程.
| 4 |
| 5 |
(2)已知双曲线的渐近线方程为y=±
| 3 |
| 4 |
| 16 |
| 5 |
考点:椭圆的标准方程,双曲线的标准方程
专题:圆锥曲线的定义、性质与方程
分析:(1)由题意设出椭圆的标准方程,结合已知及隐含条件求得a,b的值则椭圆方程可求;
(2)由已知可知双曲线的焦点在x轴上,再由已知结合隐含条件求得a,b的值,则双曲线方程可求.
(2)由已知可知双曲线的焦点在x轴上,再由已知结合隐含条件求得a,b的值,则双曲线方程可求.
解答:
解:(1)设椭圆的标准方程为:
+
=1(a>b>0),
由题意得
,解得a=5,b=3.
∴所求椭圆的标准方程为
+
=1;
(2)由题意知双曲线标准方程为:
-
=1,
∴
=
,
=
,
又c2=a2+b2,解得a=4,b=3,
∴所求双曲线标准方程为
-
=1.
| x2 |
| a2 |
| y2 |
| b2 |
由题意得
|
∴所求椭圆的标准方程为
| x2 |
| 25 |
| y2 |
| 9 |
(2)由题意知双曲线标准方程为:
| x2 |
| a2 |
| y2 |
| b2 |
∴
| b |
| a |
| 3 |
| 4 |
| a2 |
| c |
| 16 |
| 5 |
又c2=a2+b2,解得a=4,b=3,
∴所求双曲线标准方程为
| x2 |
| 16 |
| y2 |
| 9 |
点评:本题考查了圆锥曲线方程的求法,考查了椭圆、双曲线的简单几何性质,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
用数学归纳法证明“1+a+a2+…+an+1=
,(a≠1,n∈N*)”时,在验证n=1成立时,左边应该是( )
| 1-an+2 |
| 1-a |
| A、1+a+a2 |
| B、1+a+a2+a3 |
| C、1+a |
| D、1 |
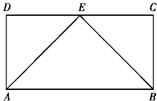 如图,矩形ABCD中,点E为边CD的中点,若在矩形中随机撒一粒黄豆,则黄豆落在△ABE内的概率为
如图,矩形ABCD中,点E为边CD的中点,若在矩形中随机撒一粒黄豆,则黄豆落在△ABE内的概率为


