题目内容
20.若a,b∈R,ab>0,则$\frac{{a}^{4}+4{b}^{4}+1}{ab}$的最小值为4.分析 【方法一】两次利用基本不等式,即可求出最小值,需要注意不等式等号成立的条件是什么.
【方法二】将$\frac{1}{ab}$拆成$\frac{1}{2ab}$+$\frac{1}{2ab}$,利用柯西不等式求出最小值.
解答 解:【解法一】a,b∈R,ab>0,
∴$\frac{{a}^{4}+4{b}^{4}+1}{ab}$≥$\frac{2\sqrt{{a}^{4}•{4b}^{4}}+1}{ab}$
=$\frac{{{4a}^{2}b}^{2}+1}{ab}$
=4ab+$\frac{1}{ab}$≥2$\sqrt{4ab•\frac{1}{ab}}$=4,
当且仅当$\left\{\begin{array}{l}{{a}^{4}={4b}^{4}}\\{4ab=\frac{1}{ab}}\end{array}\right.$,
即$\left\{\begin{array}{l}{{a}^{2}={2b}^{2}}\\{{{a}^{2}b}^{2}=\frac{1}{4}}\end{array}\right.$,
即a=$\frac{1}{\root{4}{2}}$,b=$\frac{1}{\root{4}{8}}$或a=-$\frac{1}{\root{4}{2}}$,b=-$\frac{1}{\root{4}{8}}$时取“=”;
∴上式的最小值为4.
【解法二】a,b∈R,ab>0,
∴$\frac{{a}^{4}+4{b}^{4}+1}{ab}$=$\frac{{a}^{3}}{b}$+$\frac{{4b}^{3}}{a}$+$\frac{1}{2ab}$+$\frac{1}{2ab}$≥4$\root{4}{\frac{{a}^{3}}{b}•\frac{{4b}^{3}}{a}•\frac{1}{2ab}•\frac{1}{2ab}}$=4,
当且仅当$\left\{\begin{array}{l}{{a}^{4}={4b}^{4}}\\{4ab=\frac{1}{ab}}\end{array}\right.$,
即$\left\{\begin{array}{l}{{a}^{2}={2b}^{2}}\\{{{a}^{2}b}^{2}=\frac{1}{4}}\end{array}\right.$,
即a=$\frac{1}{\root{4}{2}}$,b=$\frac{1}{\root{4}{8}}$或a=-$\frac{1}{\root{4}{2}}$,b=-$\frac{1}{\root{4}{8}}$时取“=”;
∴上式的最小值为4.
故答案为:4.
点评 本题考查了基本不等式的应用问题,是中档题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | p∧q | B. | p∧¬q | C. | ¬p∧q | D. | ¬p∧¬q |
| A. | ω=$\frac{2}{3}$,φ=$\frac{π}{12}$ | B. | ω=$\frac{2}{3}$,φ=-$\frac{11π}{12}$ | C. | ω=$\frac{1}{3}$,φ=-$\frac{11π}{24}$ | D. | ω=$\frac{1}{3}$,φ=$\frac{7π}{24}$ |
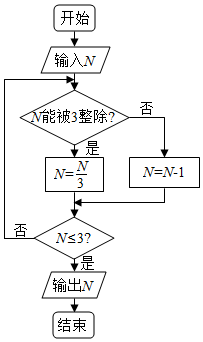
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
 如图,在三棱锥P-ABC中,PA⊥底面ABC,∠BAC=90°.点D,E,N分别为棱PA,PC,BC的中点,M是线段AD的中点,PA=AC=4,AB=2.
如图,在三棱锥P-ABC中,PA⊥底面ABC,∠BAC=90°.点D,E,N分别为棱PA,PC,BC的中点,M是线段AD的中点,PA=AC=4,AB=2.