题目内容
7.已知双曲线$\frac{{x}^{2}}{2}$-$\frac{{y}^{2}}{k}$=1的两个焦点F1、F2,其一条渐近线方程y=x,若P(m,1)在双曲线上,求$\overrightarrow{P{F}_{1}}$•$\overrightarrow{P{F}_{2}}$的值.分析 利用双曲线的渐近线方程求出k,得到双曲线方程,然后求解P的坐标,求出焦点坐标,然后求解向量的数量积.
解答 解:双曲线$\frac{{x}^{2}}{2}$-$\frac{{y}^{2}}{k}$=1的两个焦点F1、F2,其一条渐近线方程y=x,
可得k=2,若P(m,1)在双曲线上,可知:m2-1=2,m=$±\sqrt{3}$,
由双曲线的对称性,不妨取P($\sqrt{3}$,1),
双曲线$\frac{{x}^{2}}{2}$-$\frac{{y}^{2}}{2}$=1的两个焦点F1(-2,0),F2(2,0),
$\overrightarrow{P{F}_{1}}$•$\overrightarrow{P{F}_{2}}$=(-2-$\sqrt{3}$,-1)(2-$\sqrt{3}$,-1)=-(4-3)+1=0.
$\overrightarrow{P{F}_{1}}$•$\overrightarrow{P{F}_{2}}$的值为0.
点评 本题考查双曲线的简单性质的应用,向量的数量积,考查计算能力.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
16.已知函数f(x)=x3+ax2+bx有两个极值点x1、x2,且x1<x2,若x1+2x0=3x2,函数g(x)=f(x)-f(x0),则g(x)( )
| A. | 恰有一个零点 | B. | 恰有两个零点 | C. | 恰有三个零点 | D. | 至多两个零点 |
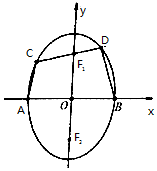 已知F1、F2分别是椭圆$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1(a>b>0)的上,下焦点,A,B分别为椭圆的左、右顶点,过椭圆的上焦点F1的直线在x轴上方部分交椭圆于C、D两点,△F2CD的周长为8,若椭圆的离心率为$\frac{\sqrt{3}}{2}$.
已知F1、F2分别是椭圆$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1(a>b>0)的上,下焦点,A,B分别为椭圆的左、右顶点,过椭圆的上焦点F1的直线在x轴上方部分交椭圆于C、D两点,△F2CD的周长为8,若椭圆的离心率为$\frac{\sqrt{3}}{2}$.