题目内容
8.在直角坐标系xOy中,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C1的极坐标方程为ρcosθ=4.(1)M为曲线C1上的动点,点P在线段OM上,且满足|OM|•|OP|=16,求点P的轨迹C2的直角坐标方程;
(2)设点A的极坐标为(2,$\frac{π}{3}$),点B在曲线C2上,求△OAB面积的最大值.
分析 (1)设P(x,y),利用相似得出M点坐标,根据|OM|•|OP|=16列方程化简即可;
(2)求出曲线C2的圆心和半径,得出B到OA的最大距离,即可得出最大面积.
解答 解:(1)曲线C1的直角坐标方程为:x=4,
设P(x,y),M(4,y0),则$\frac{x}{4}=\frac{y}{{y}_{0}}$,∴y0=$\frac{4y}{x}$,
∵|OM||OP|=16,
∴$\sqrt{{x}^{2}+{y}^{2}}$$\sqrt{16+{{y}_{0}}^{2}}$=16,
即(x2+y2)(1+$\frac{{y}^{2}}{{x}^{2}}$)=16,
∴x4+2x2y2+y4=16x2,即(x2+y2)2=16x2,
两边开方得:x2+y2=4x,
整理得:(x-2)2+y2=4(x≠0),
∴点P的轨迹C2的直角坐标方程:(x-2)2+y2=4(x≠0).
(2)点A的直角坐标为A(1,$\sqrt{3}$),显然点A在曲线C2上,|OA|=2,
∴曲线C2的圆心(2,0)到弦OA的距离d=$\sqrt{4-1}$=$\sqrt{3}$,
∴△AOB的最大面积S=$\frac{1}{2}$|OA|•(2+$\sqrt{3}$)=2+$\sqrt{3}$.
点评 本题考查了极坐标方程与直角坐标方程的转化,轨迹方程的求解,直线与圆的位置关系,属于中档题.

练习册系列答案
 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
16.从分别标有1,2,…,9的9张卡片中不放回地随机抽取2次,每次抽取1张,则抽到在2张卡片上的数奇偶性不同的概率是( )
| A. | $\frac{5}{18}$ | B. | $\frac{4}{9}$ | C. | $\frac{5}{9}$ | D. | $\frac{7}{9}$ |
13.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左焦点为F,离心率为$\sqrt{2}$.若经过F和P(0,4)两点的直线平行于双曲线的一条渐近线,则双曲线的方程为( )
| A. | $\frac{{x}^{2}}{4}-\frac{{y}^{2}}{4}$=1 | B. | $\frac{{x}^{2}}{8}-\frac{{y}^{2}}{8}$=1 | C. | $\frac{{x}^{2}}{4}-\frac{{y}^{2}}{8}$=1 | D. | $\frac{{x}^{2}}{8}-\frac{{y}^{2}}{4}$=1 |
16.已知函数f(x)=x3+ax2+bx有两个极值点x1、x2,且x1<x2,若x1+2x0=3x2,函数g(x)=f(x)-f(x0),则g(x)( )
| A. | 恰有一个零点 | B. | 恰有两个零点 | C. | 恰有三个零点 | D. | 至多两个零点 |
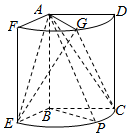 如图,几何体是圆柱的一部分,它是由矩形ABCD(及其内部)以AB边所在直线为旋转轴旋转120°得到的,G是$\widehat{DF}$的中点.
如图,几何体是圆柱的一部分,它是由矩形ABCD(及其内部)以AB边所在直线为旋转轴旋转120°得到的,G是$\widehat{DF}$的中点.