题目内容
已知f(x)=logax(a>0,a≠1)满足f[f(a2)]+f(3)=af(1)
(1)求a;
(2)计算f2(2)+f(2)f(3)+f(3)
(1)求a;
(2)计算f2(2)+f(2)f(3)+f(3)
考点:对数函数的图像与性质
专题:函数的性质及应用
分析:根据对数的运算性质化简计算即可
解答:
解:(1)f[f(a2)]+f(3)=af(1)∴f(2)+f(3)=1即loga6=1,∴a=6,
(2)f2(2)+f(2)f(3)+f(3)
=f(2)(f(2)+f(3))+f(3)
=log62(log62+log63)+log63
=log62+log63=1
(2)f2(2)+f(2)f(3)+f(3)
=f(2)(f(2)+f(3))+f(3)
=log62(log62+log63)+log63
=log62+log63=1
点评:本题考查了对数函数的运算性质,属于基础题

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知向量
=(cosθ,sinθ)和
=(
-sinθ,cosθ),θ=(π,2π),且|
+
|=
,则cos(
+
)的值是( )
| m |
| n |
| 2 |
| m |
| n |
8
| ||
| 5 |
| θ |
| 2 |
| π |
| 8 |
A、-
| ||
B、-
| ||
C、
| ||
D、
|
三条直线x=2,x-y-1=0,x+ky=0相交于一点,则实数k=( )
| A、2 | ||
B、
| ||
| C、-2 | ||
D、-
|
椭圆x2+
=1的一个焦点是(0,
),那么k=( )
| y2 |
| k |
| 5 |
| A、-6 | ||
| B、6 | ||
C、
| ||
D、1-
|
双曲线
-
=-5的一条渐近线方程是( )
| x2 |
| 4 |
| y2 |
| 9 |
| A、2x-3y=0 |
| B、3x+2y=0 |
| C、9x-4y=0 |
| D、4x-9y=0 |
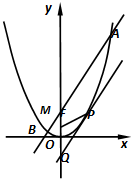 如图,设抛物线C:x2=4y的焦点为F,P(x0,y0)为抛物线上的任一点(其中x0≠0),过P点的切线交y轴于Q点.
如图,设抛物线C:x2=4y的焦点为F,P(x0,y0)为抛物线上的任一点(其中x0≠0),过P点的切线交y轴于Q点.