题目内容
若1+sinθ-25cos2θ=0,θ为锐角,求cos
的值.
| θ |
| 2 |
考点:二倍角的余弦
专题:三角函数的求值
分析:已知等式利用同角三角函数间的基本关系变形后,求出sinθ的值,进而求出cosθ的值,利用二倍角的余弦函数公式即可求出cos
的值.
| θ |
| 2 |
解答:
解:已知等式变形得:1+sinθ-25cos2θ=1+sinθ-25(1-sin2θ)=0,即25sin2θ+sinθ-24=0,
分解因式得:(sinθ+1)(25sinθ-24)=0,
解得:sinθ=-1或sinθ=
,
∵θ为锐角,即
为锐角,
∴sinθ=
,
∴cosθ=
=
,即2cos2
-1=
,
解得:cos
=
.
分解因式得:(sinθ+1)(25sinθ-24)=0,
解得:sinθ=-1或sinθ=
| 24 |
| 25 |
∵θ为锐角,即
| θ |
| 2 |
∴sinθ=
| 24 |
| 25 |
∴cosθ=
| 1-sin2θ |
| 7 |
| 25 |
| θ |
| 2 |
| 7 |
| 25 |
解得:cos
| θ |
| 2 |
| 4 |
| 5 |
点评:此题考查了二倍角的余弦函数公式,以及同角三角函数间的基本关系,熟练掌握公式是解本题的关键.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
已知函数f(x)=acosx+bx2-
x,若f′(x0)=0则f′(-x0)=( )
| 2 |
| A、0 | ||
| B、2a | ||
| C、2b | ||
D、-2
|
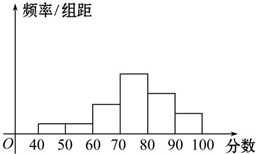 从某校参加数学竞赛的试卷中抽取一个样本,考查竞赛的成绩分布,将样本分成6组,得到频率分布直方图如图,从左到右各小组的小长方形的高的比为1:1:3:6:4:2,最右边的一组的频数是8.估计这次数学竞赛成绩的平均数
从某校参加数学竞赛的试卷中抽取一个样本,考查竞赛的成绩分布,将样本分成6组,得到频率分布直方图如图,从左到右各小组的小长方形的高的比为1:1:3:6:4:2,最右边的一组的频数是8.估计这次数学竞赛成绩的平均数