题目内容
已知函数φ(x)=lnx.
(1)若曲线g(x)=φ(x)+
-1在点(2,g(2))处的切线与直线3x+y-1=0平行,求a的值;
(2)求证函数f(x)=φ(x)-
在(0,+∞)上为单调增函数;
(3)设m,n∈R+,且m≠n,求证:
<|
|.
(1)若曲线g(x)=φ(x)+
| a |
| x |
(2)求证函数f(x)=φ(x)-
| 2(x-1) |
| x+1 |
(3)设m,n∈R+,且m≠n,求证:
| m-n |
| m+n |
| lnm-lnn |
| 2 |
考点:利用导数求闭区间上函数的最值,利用导数研究函数的单调性,利用导数研究曲线上某点切线方程
专题:证明题,导数的综合应用
分析:(1)先求出g(x)的导数g′(x),求出g′(2),根据条件得到g′(2)=-3,解出a的值;
(2)可先求出f(x)的导数f′(x),并化简整理、因式分解,由条件x>0,即可判断导数的符号,从而得证;
(3)设m>n>0,应用分析法证明,要证原不等式成立,可以适当变形,只需证
<
,然后构造函数h(x)=lnx-
(x>1),应用导数说明h(x)在(1,+∞)上是单调增函数,从而h(x)>h(1)=0,即可得证.
(2)可先求出f(x)的导数f′(x),并化简整理、因式分解,由条件x>0,即可判断导数的符号,从而得证;
(3)设m>n>0,应用分析法证明,要证原不等式成立,可以适当变形,只需证
| ||
|
ln
| ||
| 2 |
| 2(x-1) |
| x+1 |
解答:
解:(1)g(x)=ϕ(x)+
-1=lnx+
-1(x>0),g′(x)=
-
(x>0),
∵曲线g(x)=ϕ(x)+
-1在点(2,g(2))处的切线与直线3x+y-1=0平行,
∴g′(2)=
-
=-3,解得a=14;
(2)证明:f(x)=ϕ(x)-
═lnx-
(x>0),
∴f′(x)=
-
=
≥0,
∴函数f(x)=ϕ(x)-
在(0,+∞)上为单调增函数;
(3)不妨设m>n>0,则
>1,
要证
<|
|,
即证
<
,
只需证
<
,即证ln
>
,
只需证ln
-
>0,
设h(x)=lnx-
(x>1),
由(2)得,h(x)在(1,+∞)上是单调增函数,
∵x>1,∴h(x)>h(1)=0,
即ln
-
>0,
即
<
.
∴不等式
<|
|成立.
| a |
| x |
| a |
| x |
| 1 |
| x |
| a |
| x2 |
∵曲线g(x)=ϕ(x)+
| a |
| x |
∴g′(2)=
| 1 |
| 2 |
| a |
| 4 |
(2)证明:f(x)=ϕ(x)-
| 2(x-1) |
| x+1 |
| 2(x-1) |
| x+1 |
∴f′(x)=
| 1 |
| x |
| 2(x+1)-2(x-1) |
| (x+1)2 |
| (x-1)2 |
| x(x+1)2 |
∴函数f(x)=ϕ(x)-
| 2(x-1) |
| x+1 |
(3)不妨设m>n>0,则
| m |
| n |
要证
| m-n |
| m+n |
| lnm-lnn |
| 2 |
即证
| m-n |
| m+n |
| lnm-lnn |
| 2 |
只需证
| ||
|
ln
| ||
| 2 |
| m |
| n |
2(
| ||
|
只需证ln
| m |
| n |
2(
| ||
|
设h(x)=lnx-
| 2(x-1) |
| x+1 |
由(2)得,h(x)在(1,+∞)上是单调增函数,
∵x>1,∴h(x)>h(1)=0,
即ln
| m |
| n |
2(
| ||
|
即
| m-n |
| m+n |
| lnm-lnn |
| 2 |
∴不等式
| m-n |
| m+n |
| lnm-lnn |
| 2 |
点评:本题主要考查导数在函数中的应用:求单调区间、证明单调性以及不等式,考查应用导数求切线方程,以及构造函数解题的能力,是一道综合题.

练习册系列答案
相关题目
曲线f(x)=x3+2x-1在点P0处的切线平行于直线y=5x+2,则点P0坐标为( )
| A、(1,2) |
| B、(-1,-4) |
| C、(1,2)或(-1,-4) |
| D、(2,4)或(-1,-4) |
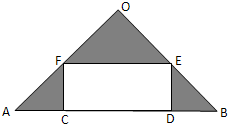 为响应党的十八大提出的文化强国建设的号召,某县政府计划建立一个文化产业园区,计划在等腰三角形OAB的空地上修建一个占地面积为S的矩形CDEF文化园展厅,如图点C、D在底边AB上,E、F分别在腰OB、OA上,已知OA=OB=30米,AB=
为响应党的十八大提出的文化强国建设的号召,某县政府计划建立一个文化产业园区,计划在等腰三角形OAB的空地上修建一个占地面积为S的矩形CDEF文化园展厅,如图点C、D在底边AB上,E、F分别在腰OB、OA上,已知OA=OB=30米,AB=