题目内容
18．
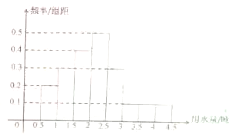某城市100户居民的月平均用水量（单位：吨），按[0.5，1），[1，1.5），[1.5，2），[2，2.5），[2.5，3），[3，3.5），[3.5，4），[4，4.5）分组的频率分布直方图如图．（1）求月平均用水量的众数和中位数；
（2）在月平均用水量为[1.5，2），[2，2.5），[2.5，3）的三组用户中，用分层抽样的方法抽取12户居民参加用水价格听证会，则月平均用水量在[2，2.5）的用户中应抽取多少户？
分析 （1）根据频率分布直方图，计算众数和中位数即可；
（2）求出月平均用水量为[1.5，2）、[2，2.5）和[2.5，3）内的用户，计算分层抽样抽取比例，
即可求出月平均用水量在[2，2.5）的用户中应抽取的户数．
解答 解：（1）根据频率分布直方图，计算月平均用水量的众数是
$\frac{2+2.5}{2}$=2.25（吨），
因为（0.2+0.3+0.4）×0.5=0.45＜0.5，
所以月均用水量的中位数在[2，2.5）内，
设中位数为x，则（0.2+0.3+0.4）×0.5+0.5×（x-2）=0.5，
x=2.1，
所以月平均用水量的中位数是2.1；
（2）月平均用水量为[1.5，2）内的用户有0.4×0.5×100=20户，
月平均用水在[2，2.5）内的用户有0.5×0.5×100=25户，
月平均用水量在[2.5，3）内的用户有0.3×0.5×100=15户，
用分层抽样的方法抽取12户，抽取比例为$\frac{12}{20+25+15}$=$\frac{1}{5}$，
所以月平均用水量在[2，2.5）的用户中应抽取25×$\frac{1}{5}$=5户．
点评 本题考查了利用频率分布直方图求众数与中位数的应用问题，也考查了分层抽样方法的应用问题，是基础题目．
练习册系列答案
相关题目
9．抛物线y2=2px（p＞0）的焦点为F，直线l过焦点F且斜率为2，与抛物线交于A、B（其中A在第一象限）两点，M（-$\frac{p}{2}$，0），则tan∠AMF=（ ）
| A． | $\frac{\sqrt{3}}{2}$ | B． | $\frac{\sqrt{3}}{3}$ | C． | $\frac{\sqrt{6}}{3}$ | D． | $\frac{2}{5}$$\sqrt{5}$ |
6．已知抛物线x2=2py（p＞0）的准线经过点（-1，-2），则抛物线的焦点坐标为（ ）
| A． | （0，2） | B． | （4，0） | C． | （0，4） | D． | （2，0） |
13．若焦点在y轴上的椭圆$\frac{{x}^{2}}{m}$+$\frac{{y}^{2}}{2}$=1的离心率为$\frac{2}{3}$，则m的值为（ ）
| A． | $\frac{8}{3}$ | B． | $\frac{2}{3}$ | C． | $\frac{10}{9}$ | D． | 以上答案均不对 |
10．若双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$（a＞0，b＞0）的一条渐近线与直线3x-y+1=0平行，则此双曲线的离心率是（ ）
| A． | $\sqrt{3}$ | B． | $2\sqrt{2}$ | C． | 3 | D． | $\sqrt{10}$ |