题目内容
3．若函数f（x）=3x2+2x-a在区间（-1，1）上有唯一零点，则实数a的取值范围是1＜a＜5或$a=-\frac{1}{3}$．分析 由题意知，函数f（x）在区间（-1，1）内有一个零点，它的对称轴为x=$-\frac{1}{3}$，得出不等式组，解出即可．
解答 解：∵函数f（x）=3x2+2x-a它的对称轴为x=$-\frac{1}{3}$，
∴函数f（x）在区间（-1，1）不是单调递增，
∵方程3x2+2x+-a=0在区间（-1，1）内有一个零点，
可得△=4+12a=0时，即a=$-\frac{1}{3}$函数有且只有一个零点．
当f（-1）f（1）＜0时，也只有一个零点，
此时：（1-a）（5-a）＜0，
解得a∈（1，5），
故答案为：1＜a＜5或$a=-\frac{1}{3}$．
点评 此题主要考查函数的零点以及二次函数的性质问题，容易得出答案，是中档题．
练习册系列答案
超能学典应用题题卡系列答案
相关题目
13．若焦点在y轴上的椭圆$\frac{{x}^{2}}{m}$+$\frac{{y}^{2}}{2}$=1的离心率为$\frac{2}{3}$，则m的值为（ ）
| A． | $\frac{8}{3}$ | B． | $\frac{2}{3}$ | C． | $\frac{10}{9}$ | D． | 以上答案均不对 |
11．已知四个关系式：$\sqrt{3}$∈R，0.2∉Q，|-3|∈N，0∈∅，其中正确的个数（ ）
| A． | 4个 | B． | 3个 | C． | 2个 | D． | 1个 |
18．已知椭圆C1和抛物线C2的焦点均在x轴上，从两条曲线上各取两个点，将其坐标混合记录于表中：
（1）求椭圆C1和抛物线C2的标准方程；
（2）过椭圆C1右焦点F的直线l与此椭圆相交于A，B两点，点P（4，0），设$\overrightarrow{FA}=λ\overrightarrow{FB}，λ∈[{-2，-1}]$，求$|{\overrightarrow{PA}+\overrightarrow{PB}}|$取最大值时，直线l的斜率．
| x | $-\sqrt{2}$ | 2 | $\sqrt{6}$ | 9 |
| y | $\sqrt{3}$ | $-\sqrt{2}$ | -1 | 3 |
（2）过椭圆C1右焦点F的直线l与此椭圆相交于A，B两点，点P（4，0），设$\overrightarrow{FA}=λ\overrightarrow{FB}，λ∈[{-2，-1}]$，求$|{\overrightarrow{PA}+\overrightarrow{PB}}|$取最大值时，直线l的斜率．
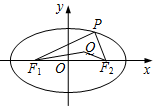在平面直角坐标系xOy中，已知椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$的左，右焦点分别为F1（-3，0），F2（3，0）．点P（x0，y0）是椭圆C在x轴上方的动点，且△PF1F2的周长为16．