题目内容
8.已知$|\overrightarrow a|=1$,$|\overrightarrow b|=1$,$\overrightarrow a$与$\overrightarrow b$的夹角为60°,那么$|2\overrightarrow a-\overrightarrow b|$=( )| A. | 2 | B. | 3 | C. | $\sqrt{3}$ | D. | $\sqrt{7}$ |
分析 运用向量数量积的定义和性质:向量的平方即为模的平方,计算即可得到所求值.
解答 解:$|\overrightarrow a|=1$,$|\overrightarrow b|=1$,$\overrightarrow a$与$\overrightarrow b$的夹角为60°,
则$\overrightarrow{a}$•$\overrightarrow{b}$=|$\overrightarrow{a}$|•|$\overrightarrow{b}$|•cos60°=1×1×$\frac{1}{2}$=$\frac{1}{2}$,
那么$|2\overrightarrow a-\overrightarrow b|$=$\sqrt{(2\overrightarrow{a}-\overrightarrow{b})^{2}}$=$\sqrt{4{\overrightarrow{a}}^{2}-4\overrightarrow{a}•\overrightarrow{b}+{\overrightarrow{b}}^{2}}$
=$\sqrt{4-4×\frac{1}{2}+1}$=$\sqrt{3}$.
故选:C.
点评 本题考查平面向量的数量积的定义和性质,主要是向量的平方即为模的平方,考查运算能力,属于基础题.

练习册系列答案
 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
18.已知双曲线C:mx2+ny2=1(mn<0)的一条渐近线与圆x2+y2-6x-2y+9=0相切,则C的离心率等于( )
| A. | $\frac{5}{3}$ | B. | $\frac{5}{4}$ | C. | $\frac{5}{3}$或$\frac{25}{16}$ | D. | $\frac{5}{3}$或$\frac{5}{4}$ |
3.圆锥过轴的截面是( )
| A. | 圆 | B. | 等腰三角形 | C. | 矩形 | D. | 抛物线 |
13.若焦点在y轴上的椭圆$\frac{{x}^{2}}{m}$+$\frac{{y}^{2}}{2}$=1的离心率为$\frac{2}{3}$,则m的值为( )
| A. | $\frac{8}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{10}{9}$ | D. | 以上答案均不对 |
18.已知椭圆C1和抛物线C2的焦点均在x轴上,从两条曲线上各取两个点,将其坐标混合记录于表中:
(1)求椭圆C1和抛物线C2的标准方程;
(2)过椭圆C1右焦点F的直线l与此椭圆相交于A,B两点,点P(4,0),设$\overrightarrow{FA}=λ\overrightarrow{FB},λ∈[{-2,-1}]$,求$|{\overrightarrow{PA}+\overrightarrow{PB}}|$取最大值时,直线l的斜率.
| x | $-\sqrt{2}$ | 2 | $\sqrt{6}$ | 9 |
| y | $\sqrt{3}$ | $-\sqrt{2}$ | -1 | 3 |
(2)过椭圆C1右焦点F的直线l与此椭圆相交于A,B两点,点P(4,0),设$\overrightarrow{FA}=λ\overrightarrow{FB},λ∈[{-2,-1}]$,求$|{\overrightarrow{PA}+\overrightarrow{PB}}|$取最大值时,直线l的斜率.
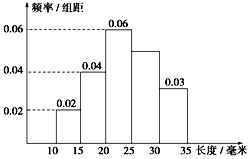 对一批零件的长度(单位:mm)进行抽样检测,检测结果的频率分布直方图如图所示.根据标准,零件长度在区间[20,25)上的为一等品,在区间[15,20)和区间[25,30)上的为二等品,在区间[10,15)和[30,35)上的为三等品.
对一批零件的长度(单位:mm)进行抽样检测,检测结果的频率分布直方图如图所示.根据标准,零件长度在区间[20,25)上的为一等品,在区间[15,20)和区间[25,30)上的为二等品,在区间[10,15)和[30,35)上的为三等品. 国庆期间,高速公路堵车现象经常发生.某调查公司为了了解车速,在赣州西收费站从7座以下小型汽车中按进收费站的先后顺序,每间隔50辆就抽取一辆的抽样方法抽取40辆汽车进行抽样调查,将他们在某段高速公路的车速(km/h))分成六段[60,65),[65,70),[70,75),[75,80),[80,85),[85,90]后,得到如图的频率分布直方图.
国庆期间,高速公路堵车现象经常发生.某调查公司为了了解车速,在赣州西收费站从7座以下小型汽车中按进收费站的先后顺序,每间隔50辆就抽取一辆的抽样方法抽取40辆汽车进行抽样调查,将他们在某段高速公路的车速(km/h))分成六段[60,65),[65,70),[70,75),[75,80),[80,85),[85,90]后,得到如图的频率分布直方图.