题目内容
用穿根法的图象做出h(x)=-3+
,指出函数在区间 >0,区间 <0.
| 1 |
| x2 |
考点:函数的图象
专题:计算题,作图题,函数的性质及应用
分析:由题意因式分解,从而用穿根法求得答案.
解答:
解:h(x)=-3+
=-3
;
则作数轴如下,

又∵h(x)=-3
前有负号;
故函数在区间(-
,
)上大于0,
在(-∞,-
),(
,+∞)上小于0;
故答案为:(-
,
);(-∞,-
),(
,+∞).
| 1 |
| x2 |
(x-
| ||||||||
| x2 |
则作数轴如下,

又∵h(x)=-3
(x-
| ||||||||
| x2 |
故函数在区间(-
| ||
| 3 |
| ||
| 3 |
在(-∞,-
| ||
| 3 |
| ||
| 3 |
故答案为:(-
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
点评:本题考查了学生对穿根法的理解与掌握,属于基础题.

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
已知命题p:“?x∈R,总有x2-x+1>0”的否定是“?x∈R,使得x2-x+1≤0”;命题q:在△ABC中,“A>
”是“sinA>
”的必要不充分条件.则有( )
| π |
| 4 |
| ||
| 2 |
| A、p真q真 | B、p真q假 |
| C、p假q真 | D、p假q假 |
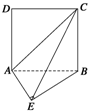 如图所示,在直二面角D-AB-E中,四边形ABCD是边长为2的正方形,△AEB是等腰直角三角形,其中∠AEB=90°,则点D到平面ACE的距离为( )
如图所示,在直二面角D-AB-E中,四边形ABCD是边长为2的正方形,△AEB是等腰直角三角形,其中∠AEB=90°,则点D到平面ACE的距离为( )