题目内容
在四面体ABCD中，AB=CD=6，BC=AC=AD=BD=5，则该四面体外接球的表面积 ．
考点：球内接多面体
专题：计算题,空间位置关系与距离
分析：分别取AB，CD的中点E，F，连接相应的线段，由条件可知，球心G在EF上，可以证明G为EF中点，求出球的半径，然后求出球的表面积．
解答：
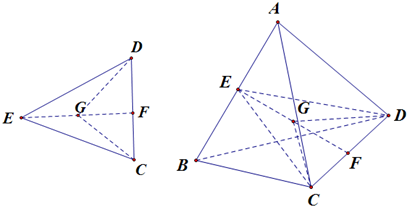解：分别取AB，CD的中点E，F，连接相应的线段CE，ED，EF，由条件，AB=CD=4，BC=AC=AD=BD=5，可知，△ABC与△ADB，都是等腰三角形，
AB⊥平面ECD，∴AB⊥EF，同理CD⊥EF，∴EF是AB与CD的公垂线，球心G在EF上，可以证明G为EF中点，（△AGB≌△CGD）
DE=
=4，DF=3，EF=
=
，
∴GF=
，
球半径DG=
=
，
∴外接球的表面积为4π×DG2=43π，
故答案为：43π．
解：分别取AB，CD的中点E，F，连接相应的线段CE，ED，EF，由条件，AB=CD=4，BC=AC=AD=BD=5，可知，△ABC与△ADB，都是等腰三角形，AB⊥平面ECD，∴AB⊥EF，同理CD⊥EF，∴EF是AB与CD的公垂线，球心G在EF上，可以证明G为EF中点，（△AGB≌△CGD）
DE=
| 25-9 |
| 16-9 |
| 7 |
∴GF=
| ||
| 2 |
球半径DG=
|
| ||
| 2 |
∴外接球的表面积为4π×DG2=43π，
故答案为：43π．
点评：本题考查球的内接几何体，球的表面积的求法，考查计算能力．
练习册系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
重庆实验外国语学校高二年级将从个班推选出来的6个男生，5个女生中任选3人组建“重外学生文明督察岗”，则下列事件中互斥不对立的事件是（ ）
| A、“3个都是男生”和“至多1个女生” |
| B、“至少有2个男生”和“至少两个女生” |
| C、“恰有2个女生”和“恰有1个或3个男生” |
| D、“至少有2个女生”和“恰有2个男生” |
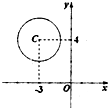已知圆C：（x+3）2+（y-4）2=4