题目内容
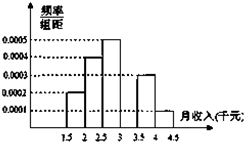某调查机构就某单位一千多名职工的月收入进行调查，现从中随机抽出100名，已知抽到的职工的月收入都在[1500，4500）元之间，根据调查结果得出职工的月收入情况残缺的频率分布直方图如图所示，则该单位职工的月收入的平均数大约是考点：频率分布直方图
专题：概率与统计
分析：根据小矩形的面积为该组的频率，所有概率和为1，从而求出月收入在[3000，3500）元之间的频率，最后根据平均数公式可求出所求．
解答：
解：收入在[3000，3500）元之间的频率等于1-（0.0002+0.0004+0.0005+0.0003+0.0001）×500=0.25
月收入的平均数大约是（0.0002×1.75+0.0004×2.25+0.0005×2.75+0.0005×3.25+0.0003×3.75+0.0001×4.25）×500=3150
故答案为：3150．
月收入的平均数大约是（0.0002×1.75+0.0004×2.25+0.0005×2.75+0.0005×3.25+0.0003×3.75+0.0001×4.25）×500=3150
故答案为：3150．
点评：本题主要考查了频率分布直方图，以及平均数的估计，同时考查了识图能力，以及公式的应用，属于基础题．
练习册系列答案
芝麻开花课程新体验系列答案
怎样学好牛津英语系列答案
相关题目
将直线2x-y+λ=0沿x轴向左平移一个单位，所得直线与曲线C：
（θ为参数）相切，则实数λ的值为（ ）
|
| A、-7或3 | B、-2或8 |
| C、0或10 | D、1或11 |
下表提供了某厂节能降耗技术改造后在生产甲产品过程中记录的产量x（吨）与相应的生产能耗y（吨）的几组对应数据：
若根据上表提供的数据用最小二乘法可求得y对x的回归直线方程是
=0.7x+0.35，则表中m的值为（ ）
| x | 3 | 4 | 5 | 6 |
| y | 2.5 | 3 | m | 4.5 |
| ∧ |
| y |
| A、4 | B、4.5 | C、3 | D、3.5 |
A为y轴上异于原点O的定点，过动点P作x轴的垂线交x轴于点B，动点P满足|
+
|=2|
|，则点P的轨迹为（ ）
| PA |
| PO |
| PB |
| A、圆 | B、椭圆 | C、双曲线 | D、抛物线 |
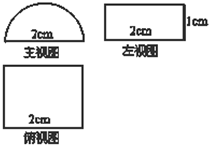已知某个几何体的三视图如图（主视图中的弧线是半圆），根据图中标出的尺寸，可得这个几何体的表面积是（ ）（单位cm）| A、6+2π | B、4+2π |
| C、6+3π | D、4+3π |