题目内容
已知f(x)=2sinx(cosx-sinx),其中x∈R,
(1)求函数f(x)的最小正周期,并指出函数y=sin2x的图象如何变换成y=f(x)的图象;(要求变换的先后顺序)
(2)在△ABC中角A,B,C对应边分别为a,b,c,f(A)=0,b=4,S△ABC=6,求a的长.
(1)求函数f(x)的最小正周期,并指出函数y=sin2x的图象如何变换成y=f(x)的图象;(要求变换的先后顺序)
(2)在△ABC中角A,B,C对应边分别为a,b,c,f(A)=0,b=4,S△ABC=6,求a的长.
考点:三角函数中的恒等变换应用,正弦定理的应用
专题:综合题,三角函数的图像与性质,解三角形
分析:(1)利用三角函数中的恒等变换可求得f(x)=
sin(2x+
)-1,从而可求得函数f(x)的最小正周期;利用三角函数y=Asin(ωx+φ)的图象变换即可求得函数y=sin2x的图象如何变换成y=f(x)的图象的;
(2)由f(A)=0可求得A=
,再由b=4,S△ABC=6可求得c=3
,利用余弦定理即可求得a.
| 2 |
| π |
| 4 |
(2)由f(A)=0可求得A=
| π |
| 4 |
| 2 |
解答:
解:(1)∵f(x)=2sinx(cosx-sinx)
=sin2x-(1-cos2x)
=sin2x+cos2x-1
=
sin(2x+
)-1,
∴函数f(x)的最小正周期T=
=π;
要得到y=sin2x的图象,需将函数f(x)的图象作如下变换:
先将y=f(x)=
sin(2x+
)-1的图象向右平移
个单位,得到y=
sin2x-1的图象,
再将y=
sin2x-1的图象向上平移1个单位,得到y=
sin2x的图象,
最后将y=
sin2x的图象的所有点的纵坐标变为原来的
倍(横坐标不变),
即可得到函数y=sin2x的图象.
(2)在△ABC中,∵f(A)=
sin(2A+
)-1=0,
∴sin(2A+
)=
,0<A<π,
∴
<2A+
<
,
∴2A+
=
,
∴A=
;
又△ABC中,b=4,S△ABC=
bcsinA=
×4c×
=6,
∴c=3
,
∴a2=b2+c2-2bccosA=16+18-2×4×3
×
=10,
∴a=
.
=sin2x-(1-cos2x)
=sin2x+cos2x-1
=
| 2 |
| π |
| 4 |
∴函数f(x)的最小正周期T=
| 2π |
| 2 |
要得到y=sin2x的图象,需将函数f(x)的图象作如下变换:
先将y=f(x)=
| 2 |
| π |
| 4 |
| π |
| 8 |
| 2 |
再将y=
| 2 |
| 2 |
最后将y=
| 2 |
| ||
| 2 |
即可得到函数y=sin2x的图象.
(2)在△ABC中,∵f(A)=
| 2 |
| π |
| 4 |
∴sin(2A+
| π |
| 4 |
| ||
| 2 |
∴
| π |
| 4 |
| π |
| 4 |
| 9π |
| 4 |
∴2A+
| π |
| 4 |
| 3π |
| 4 |
∴A=
| π |
| 4 |
又△ABC中,b=4,S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
∴c=3
| 2 |
∴a2=b2+c2-2bccosA=16+18-2×4×3
| 2 |
| ||
| 2 |
∴a=
| 10 |
点评:本题考查三角函数中的恒等变换,着重考查三角函数y=Asin(ωx+φ)的图象变换及正弦定理与余弦定理的综合应用,属于中档题.

练习册系列答案
相关题目
在长为4的线段上任取一点,则该点到两端点的距离均不小于1的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
一个空间几何体的三视图如图所示,则该几何体的体积为( )


A、
| ||
| B、3πcm3 | ||
C、
| ||
D、
|
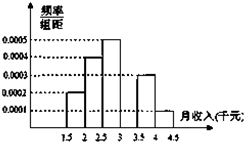 某调查机构就某单位一千多名职工的月收入进行调查,现从中随机抽出100名,已知抽到的职工的月收入都在[1500,4500)元之间,根据调查结果得出职工的月收入情况残缺的频率分布直方图如图所示,则该单位职工的月收入的平均数大约是
某调查机构就某单位一千多名职工的月收入进行调查,现从中随机抽出100名,已知抽到的职工的月收入都在[1500,4500)元之间,根据调查结果得出职工的月收入情况残缺的频率分布直方图如图所示,则该单位职工的月收入的平均数大约是