题目内容
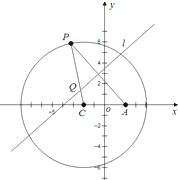 如图,圆C:(x+2)2+y2=36,P是圆C上的任意一动点,A点坐标为(2,0),线段PA的垂直平分线l与半径CP交于点Q.
如图,圆C:(x+2)2+y2=36,P是圆C上的任意一动点,A点坐标为(2,0),线段PA的垂直平分线l与半径CP交于点Q.(1)求点Q的轨迹G的方程;
(2)已知B,D是轨迹G上不同的两个任意点,M为BD的中点.①若M的坐标为M(2,1),求直线BD所在的直线方程;②若BD不经过原点,且不垂直于x轴,点O为轨迹G的中心.
求证:直线BD和直线OM的斜率之积是常数(定值).
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)结合已知条件根据椭圆的定义,点Q的轨迹G是中心在原点,以C、A为焦点,长轴长等于6的椭圆,由此能求出点Q的轨迹G的方程.
(2)①设B、D的坐标分别为(x1,y1)、(x2,y2),利用点差法能求出BD所在的直线方程.
②设B(x1,y1),D(x2,y2),由已知条件推导出kBD=
=-
,kOM=
,由此能证明直线BD和直线OM的斜率之积是常数.
(2)①设B、D的坐标分别为(x1,y1)、(x2,y2),利用点差法能求出BD所在的直线方程.
②设B(x1,y1),D(x2,y2),由已知条件推导出kBD=
| y1-y2 |
| x1-x2 |
| 5(x1+x2) |
| 9(y1+y2) |
| y1+y2 |
| x1+x2 |
解答:
(本小题满分14分)
解:(1)圆C的圆心为C(-2,0),半径r=6,|CA|=4.(1分)
连结QA,由已知得|QA|=|QP|,(2分)
∵|QC|+|QA|=|QC|+|QP|=CP=r=6>|CA|.(3分)
根据椭圆的定义,点Q的轨迹G是中心在原点,以C、A为焦点,长轴长等于6的椭圆,
即a=3,c=2,b2=a2-c2=9-4=5,(4分)
∴点Q的轨迹G的方程为
+
=1.(5分)
(2)①设B、D的坐标分别为(x1,y1)、(x2,y2),
则
(6分)
两式相减,得5(x1-x2)(x1+x2)+9(y1-y2)(y1+y2)=0,(7分)
当BD的中点M的坐标为(2,1)时,有
,(8分)
∴20(x1-x2)+18(y1-y2)=0,即kBD=
=-
.(9分)
∴BD所在的直线方程为y-1=-
(x-2),即10x+9y-29=0.(10分)
②证明:设B(x1,y1),D(x2,y2),且x1≠x2,
由①可知kBD=
=-
,(11分)
又kOM=
(12分)
∴kBD•kOM=-
×
=-
(定值).(14分)
解:(1)圆C的圆心为C(-2,0),半径r=6,|CA|=4.(1分)
连结QA,由已知得|QA|=|QP|,(2分)
∵|QC|+|QA|=|QC|+|QP|=CP=r=6>|CA|.(3分)
根据椭圆的定义,点Q的轨迹G是中心在原点,以C、A为焦点,长轴长等于6的椭圆,
即a=3,c=2,b2=a2-c2=9-4=5,(4分)
∴点Q的轨迹G的方程为
| x2 |
| 9 |
| y2 |
| 5 |
(2)①设B、D的坐标分别为(x1,y1)、(x2,y2),
则
|
两式相减,得5(x1-x2)(x1+x2)+9(y1-y2)(y1+y2)=0,(7分)
当BD的中点M的坐标为(2,1)时,有
|
∴20(x1-x2)+18(y1-y2)=0,即kBD=
| y1-y2 |
| x1-x2 |
| 10 |
| 9 |
∴BD所在的直线方程为y-1=-
| 10 |
| 9 |
②证明:设B(x1,y1),D(x2,y2),且x1≠x2,
由①可知kBD=
| y1-y2 |
| x1-x2 |
| 5(x1+x2) |
| 9(y1+y2) |
又kOM=
| y1+y2 |
| x1+x2 |
∴kBD•kOM=-
| 5(x1+x2) |
| 9(y1+y2) |
| y1+y2 |
| x1+x2 |
| 5 |
| 9 |
点评:本题考查点的轨迹方程的求法,考查直线方程的求法,考查两直线的斜率之积为常数的证明,解题时要认真审题,注意点差法的合理运用.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案
相关题目