题目内容
已知sinθ,cosθ是方程8x2+6kx+2k+1=0的两个根
(1)求实数k的值;
(2)求以tanθ,cotθ为根的一元二次方程.
(1)求实数k的值;
(2)求以tanθ,cotθ为根的一元二次方程.
考点:同角三角函数基本关系的运用
专题:函数的性质及应用
分析:(1)利用根与系数之间的关系,建立条件方程,即可求实数k的值;
(2)利用根与系数之间的关系求出tanθ+cotθ和tanθcotθ的值,即可得到对应的一元二次方程.
(2)利用根与系数之间的关系求出tanθ+cotθ和tanθcotθ的值,即可得到对应的一元二次方程.
解答:
解:(1)∵sinθ,cosθ是方程8x2+6kx+2k+1=0的两个根
∴sinθcosθ=
,…①
sinθ+cosθ=-
…②
②平方得:1+2sinθcosθ=
k2,把①代入解得:
9k2-8k-20=0,
解得k=2或-
,
又∵△≥0,得:9k2-16k-8≥0,
检验得k=2舍去,k=-
符合;
(2)依题意,得sinθcosθ=-
…③
sinθ+cosθ=
…④
则tanθ+cotθ=
+
=
=-
,
∴tanθcotθ=1,
∴以tanθ,cotθ为根的一元二次方程为x2-(tanθ+cotθ)x+tanθcotθ=0,
即x2+
x+1=0,即11x2+72x+11=0.
∴sinθcosθ=
| 2k+1 |
| 8 |
sinθ+cosθ=-
| 3k |
| 4 |
②平方得:1+2sinθcosθ=
| 9 |
| 12 |
9k2-8k-20=0,
解得k=2或-
| 10 |
| 9 |
又∵△≥0,得:9k2-16k-8≥0,
检验得k=2舍去,k=-
| 10 |
| 9 |
(2)依题意,得sinθcosθ=-
| 11 |
| 72 |
sinθ+cosθ=
| 5 |
| 6 |
则tanθ+cotθ=
| sinθ |
| cosθ |
| cosθ |
| sinθ |
| 1 |
| sinθcosθ |
| 72 |
| 11 |
∴tanθcotθ=1,
∴以tanθ,cotθ为根的一元二次方程为x2-(tanθ+cotθ)x+tanθcotθ=0,
即x2+
| 72 |
| 11 |
点评:本题主要考查根与系数之间的关系的应用,利用三角函数的基本关系式是解决本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
运行如图所示的程序框图,则输出的所有实数对(x,y)所对应的点都在函数( )
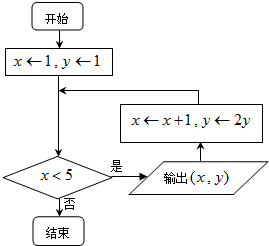

| A、y=x+1的图象上 |
| B、y=2x的图象上 |
| C、y=2x的图象上 |
| D、y=2x-1的图象上 |
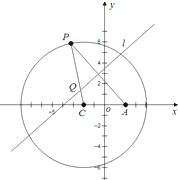 如图,圆C:(x+2)2+y2=36,P是圆C上的任意一动点,A点坐标为(2,0),线段PA的垂直平分线l与半径CP交于点Q.
如图,圆C:(x+2)2+y2=36,P是圆C上的任意一动点,A点坐标为(2,0),线段PA的垂直平分线l与半径CP交于点Q.