题目内容
已知数列{an}满足:an+1=|an-3|+1 (n∈N)
(1)若a1=0,求数列{an}的前n项和Sn;
(2)试探求a1的值,使得数列{an}成等差数列.
(1)若a1=0,求数列{an}的前n项和Sn;
(2)试探求a1的值,使得数列{an}成等差数列.
考点:数列递推式
专题:计算题,等差数列与等比数列
分析:(1)求出a2=4,a3=a4=a5=…=2,即可求数列{an}的前n项和Sn;
(2)由(1)知,a3=a4=a5=…=2,可得结论.
(2)由(1)知,a3=a4=a5=…=2,可得结论.
解答:
解:(1)∵a1=0,an+1=|an-3|+1,
∴a2=4,a3=a4=a5=…=2,
∴Sn=0+4+2(n-2)=2n;
(2)由(1)知,a3=a4=a5=…=2,
∴a1=a2=2时,数列{an}成等差数列.
∴a2=4,a3=a4=a5=…=2,
∴Sn=0+4+2(n-2)=2n;
(2)由(1)知,a3=a4=a5=…=2,
∴a1=a2=2时,数列{an}成等差数列.
点评:本题考查数列递推式,考查数列的求和,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 某通讯公司需要在三角形地带OAC区域内建造甲、乙两种通信信号加强中转站,甲中转站建在区域BOC内,乙中转站建在区域AOB内.分界线OB固定,且OB=
某通讯公司需要在三角形地带OAC区域内建造甲、乙两种通信信号加强中转站,甲中转站建在区域BOC内,乙中转站建在区域AOB内.分界线OB固定,且OB=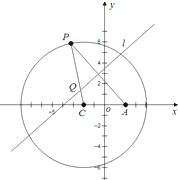 如图,圆C:(x+2)2+y2=36,P是圆C上的任意一动点,A点坐标为(2,0),线段PA的垂直平分线l与半径CP交于点Q.
如图,圆C:(x+2)2+y2=36,P是圆C上的任意一动点,A点坐标为(2,0),线段PA的垂直平分线l与半径CP交于点Q.