题目内容
已知函数f(x)=sin(
x)+1,求f(1)+f(2)+f(3)+…f(2011)的值.
| π |
| 2 |
考点:运用诱导公式化简求值
专题:三角函数的求值
分析:分别将x=1,2,3,4,5,6,…,代入f(x)求出f(1),f(2),f(3),…,的值,归纳总结得到一般性规律,即可确定出所求式子的值.
解答:
解:当x=1时,f(1)=sin
+1=1+1=2;
当x=2时,f(2)=sinπ+1=0+1=1;
当x=3时,f(3)=sin
+1=-1+1=0;
当x=4时,f(4)=sin2π+1=0+1=1;
当x=5时,f(5)=sin
+1=1+1=2;
当x=6时,f(6)=sin3π+1=0+1=1;
…,
以此类推,其中以2,1,0,1循环,
∵2011=4×502+3,
∴f(1)+f(2)+f(3)+…f(2011)=4+4+…+4+3=4×502+3=2008+3=2011.
| π |
| 2 |
当x=2时,f(2)=sinπ+1=0+1=1;
当x=3时,f(3)=sin
| 3π |
| 2 |
当x=4时,f(4)=sin2π+1=0+1=1;
当x=5时,f(5)=sin
| 5π |
| 2 |
当x=6时,f(6)=sin3π+1=0+1=1;
…,
以此类推,其中以2,1,0,1循环,
∵2011=4×502+3,
∴f(1)+f(2)+f(3)+…f(2011)=4+4+…+4+3=4×502+3=2008+3=2011.
点评:此题考查了运用诱导公式化简求值,熟练掌握诱导公式是解本题的关键.

练习册系列答案
相关题目
 某通讯公司需要在三角形地带OAC区域内建造甲、乙两种通信信号加强中转站,甲中转站建在区域BOC内,乙中转站建在区域AOB内.分界线OB固定,且OB=
某通讯公司需要在三角形地带OAC区域内建造甲、乙两种通信信号加强中转站,甲中转站建在区域BOC内,乙中转站建在区域AOB内.分界线OB固定,且OB=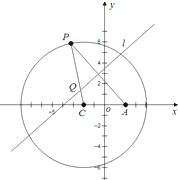 如图,圆C:(x+2)2+y2=36,P是圆C上的任意一动点,A点坐标为(2,0),线段PA的垂直平分线l与半径CP交于点Q.
如图,圆C:(x+2)2+y2=36,P是圆C上的任意一动点,A点坐标为(2,0),线段PA的垂直平分线l与半径CP交于点Q.