题目内容
已知函数y=kx+2（k≠0）在1≤x＜3时的最小值为5，求k值．
考点：一次函数的性质与图象
专题：函数的性质及应用
分析：利用分类讨论的方法，判定k＞0时，k＜0时，y=kx+2在1≤x＜3上的最值情况，求出k的值．
解答：
解：∵函数y=kx+2（k≠0），
当k＞0时，y=kx+2是定义域上的增函数，在1≤x＜3时有最小值，∴k+2=5，∴k=3．
当k＜0时，y=kx+2是定义域上的减函数，在1≤x＜3时无最小值，∴k不存在．
综上，k的值是3．
当k＞0时，y=kx+2是定义域上的增函数，在1≤x＜3时有最小值，∴k+2=5，∴k=3．
当k＜0时，y=kx+2是定义域上的减函数，在1≤x＜3时无最小值，∴k不存在．
综上，k的值是3．
点评：本题考查了一次函数的图象与性质的应用问题，解题时应用一次函数的图象与性质，按分类讨论的方法解答，是基础题．
练习册系列答案
相关题目
某通讯公司需要在三角形地带OAC区域内建造甲、乙两种通信信号加强中转站，甲中转站建在区域BOC内，乙中转站建在区域AOB内．分界线OB固定，且OB=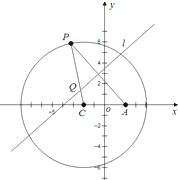
如图，圆C：（x+2）2+y2=36，P是圆C上的任意一动点，A点坐标为（2，0），线段PA的垂直平分线l与半径CP交于点Q．