题目内容
解方程组:
.
|
考点:组合及组合数公式
专题:计算题
分析:根据题意,由①式可得x=3y,将其代入②式,变形可得关于y的方程,解可得y的值,由x=3y可得答案.
解答:
解:根据题意,
,
由
=
可得,x=y+2y=3y或y=0(舍去),③
将③代入②可得:
=
,
即
=
;
变形可得7y+7=8y+4,
解可得y=3,x=3y=9;
故该方程组的解为
.
|
由
| C | y x |
| C | 2y x |
将③代入②可得:
| C | y+1 3y |
| 7 |
| 2 |
| C | y-1 3y |
即
| (3y)! |
| (3y-y-1)!×(y+1)! |
| 7 |
| 2 |
| (3y)! |
| (3y-y+1)!×(y-1)! |
变形可得7y+7=8y+4,
解可得y=3,x=3y=9;
故该方程组的解为
|
点评:本题考查组合数公式的计算与应用,灵活运用组合数公式是解题的关键.

练习册系列答案
相关题目
 某通讯公司需要在三角形地带OAC区域内建造甲、乙两种通信信号加强中转站,甲中转站建在区域BOC内,乙中转站建在区域AOB内.分界线OB固定,且OB=
某通讯公司需要在三角形地带OAC区域内建造甲、乙两种通信信号加强中转站,甲中转站建在区域BOC内,乙中转站建在区域AOB内.分界线OB固定,且OB=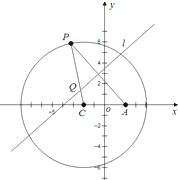 如图,圆C:(x+2)2+y2=36,P是圆C上的任意一动点,A点坐标为(2,0),线段PA的垂直平分线l与半径CP交于点Q.
如图,圆C:(x+2)2+y2=36,P是圆C上的任意一动点,A点坐标为(2,0),线段PA的垂直平分线l与半径CP交于点Q.