题目内容
已知数列{bn}的通项公式为bn=
，求证：b1+b2+…+bn＜3．
| 4(n+1) |
| 3n-1(4n2-1) |
考点：数列与不等式的综合,数列的求和
专题：等差数列与等比数列
分析：当n≥5时，bn=
＜
=
＜
，再利用等比数列的前n项和公式即可得出．
| 4(n+1) |
| 3n-1(4n2-1) |
| 4(n+1) |
| 3n-1(4n2-4) |
| 1 |
| 3n-1(n-1) |
| 1 |
| 3n |
解答：
证明：b1=
，b2=
，b3=
，b4=
．
当n≥5时，bn=
＜
=
＜
，
∴b1+b2+…+bn＜
+
+
+
+
＜
+
+
+
+
＜3．
| 8 |
| 3 |
| 4 |
| 15 |
| 16 |
| 315 |
| 20 |
| 1701 |
当n≥5时，bn=
| 4(n+1) |
| 3n-1(4n2-1) |
| 4(n+1) |
| 3n-1(4n2-4) |
| 1 |
| 3n-1(n-1) |
| 1 |
| 3n |
∴b1+b2+…+bn＜
| 8 |
| 3 |
| 4 |
| 15 |
| 16 |
| 315 |
| 20 |
| 1701 |
| ||||
1-
|
| 8 |
| 3 |
| 4 |
| 15 |
| 16 |
| 315 |
| 20 |
| 1701 |
| 1 |
| 162 |
点评：本题考查了等比数列的前n项和公式与“放缩法”，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
设向量
=（sinα，
）的模为
，则cos2α=（ ）
| a |
| ||
| 2 |
| ||
| 2 |
A、
| ||||
B、
| ||||
C、-
| ||||
D、-
|
如果直线l⊥平面α，①若直线m⊥l，则m∥α；②若m⊥α，则m∥l；③若m∥α，则m⊥l；④若m∥l，则m⊥α，上述判断正确的是 （ ）
| A、①②③ | B、②③④ |
| C、①③④ | D、②④ |
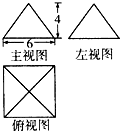
若几何体的三视图如图所示，则该几何体的体积为（ ）
A、
| ||
B、
| ||
C、
| ||
| D、π |