题目内容
如果直线l⊥平面α,①若直线m⊥l,则m∥α;②若m⊥α,则m∥l;③若m∥α,则m⊥l;④若m∥l,则m⊥α,上述判断正确的是 ( )
| A、①②③ | B、②③④ |
| C、①③④ | D、②④ |
考点:空间中直线与平面之间的位置关系
专题:空间位置关系与距离
分析:在①中也有可能m?α;由直线与平面垂直的性质定理得②③正确;由直线与平面垂直的判定定理得④正确.
解答:
解:由直线l⊥平面α,知:
①若直线m⊥l,则m∥α或m?α,故①错误;
②若m⊥α,则由直线与平面垂直的性质定理得m∥l,故②正确;
③若m∥α,则由直线与平面垂直的性质定理得m⊥l,故③正确;
④若m∥l,则由直线与平面垂直的判定定理得m⊥α,故④正确.
故选:B.
①若直线m⊥l,则m∥α或m?α,故①错误;
②若m⊥α,则由直线与平面垂直的性质定理得m∥l,故②正确;
③若m∥α,则由直线与平面垂直的性质定理得m⊥l,故③正确;
④若m∥l,则由直线与平面垂直的判定定理得m⊥α,故④正确.
故选:B.
点评:本题考查命题真假的判断,是中档题,解题时要注意空间中线线、线面、面面间的位置关系的合理运用.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
若函数f(x)满足f(x)=elnx+x2f(1)+x,则f(1)的值为( )
| A、-2e-1 | B、-e-1 |
| C、-1 | D、e+1 |
过原点O的直线MN与双曲线C:
-
=1交于M、N两点,P是双曲线C上异于M、N的点,若直线PM,PN的斜率之积kPM•kPN=
,则双曲线C的离心率e=( )
| x2 |
| a2 |
| y2 |
| b2 |
| 5 |
| 4 |
A、
| ||
B、
| ||
C、
| ||
| D、2 |
在空间,下列命题中正确的是 ( )
| A、没有公共点的两条直线平行 |
| B、与同一直线垂直的两条直线平行 |
| C、平行于同一直线的两条直线平行 |
| D、已知直线a不在平面α内,则直线a∥平面α |
已知正方体ABCD-A1B1C1D1,E、F分别是AB、AD中点,则异面直线EF与A1C1所成的角为( )
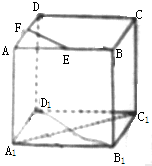

| A、30° | B、45° |
| C、60° | D、90° |
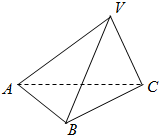 如图,三棱锥V-ABC的底面是以B为直角顶点的等腰直角三角形,侧面VAC与底面ABC垂直,已知其正视图的面积为2
如图,三棱锥V-ABC的底面是以B为直角顶点的等腰直角三角形,侧面VAC与底面ABC垂直,已知其正视图的面积为2