题目内容
求下列各曲线的标准方程.
(1)虚轴长为12,离心率为
,焦点在x轴上的双曲线;
(2)抛物线的焦点是双曲线16x2-9y2=144的左顶点.
(1)虚轴长为12,离心率为
| 5 |
| 4 |
(2)抛物线的焦点是双曲线16x2-9y2=144的左顶点.
考点:双曲线的标准方程,抛物线的标准方程
专题:圆锥曲线的定义、性质与方程
分析:(1)由题意求出双曲线的虚轴长,再由双曲线的离心率结合隐含条件求得双曲线的实轴长,则双曲线方程可求;
(2)由双曲线方程求出双曲线的左顶点坐标,从而得到抛物线的焦点坐标,则抛物线方程可求.
(2)由双曲线方程求出双曲线的左顶点坐标,从而得到抛物线的焦点坐标,则抛物线方程可求.
解答:
解:(1)由题意知,2b=12,b=6,又
=
,且a2+36=c2,解得:a2=64.
∴双曲线方程为
-
=1;
(2)由16x2-9y2=144,得
-
=1,
∴双曲线16x2-9y2=144的左顶点为(-3,0),
由抛物线的焦点是双曲线16x2-9y2=144的左顶点,可得抛物线方程为y2=-2px(p>0),且
=3,p=6.
∴抛物线方程为y2=-12x.
| c |
| a |
| 5 |
| 4 |
∴双曲线方程为
| x2 |
| 64 |
| y2 |
| 36 |
(2)由16x2-9y2=144,得
| x2 |
| 9 |
| y2 |
| 16 |
∴双曲线16x2-9y2=144的左顶点为(-3,0),
由抛物线的焦点是双曲线16x2-9y2=144的左顶点,可得抛物线方程为y2=-2px(p>0),且
| p |
| 2 |
∴抛物线方程为y2=-12x.
点评:本题考查了双曲线及抛物线方程的求法,考查了圆锥曲线的简单几何性质,是基础题.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
下列不等式不成立的是( )
| A、a2+b2+c2≥ab+bc+ca | ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
若m>n>0,则下列不等式正确的是( )
| A、2m<2n | ||||
| B、log0.2m>log0.2n | ||||
| C、am>an(0<a<1) | ||||
D、m-
|
已知命题p:不等式ax<1的解集为(0,+∞),q:函数f(x)=
在区间(0,+∞)单调递减,若p且q为假,非p为假,则a的取值范围为( )
| 1-2a |
| x |
A、(0,
| ||
B、[
| ||
| C、(0,1) | ||
| D、(1,2] |
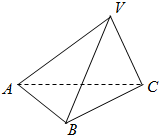 如图,三棱锥V-ABC的底面是以B为直角顶点的等腰直角三角形,侧面VAC与底面ABC垂直,已知其正视图的面积为2
如图,三棱锥V-ABC的底面是以B为直角顶点的等腰直角三角形,侧面VAC与底面ABC垂直,已知其正视图的面积为2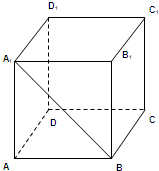 如图,ABCD-A1B1C1D1为正方体.
如图,ABCD-A1B1C1D1为正方体.