题目内容
二次函数f(x)的二次项系数为负,且对任意实数x,恒有f(x)=f(4-x),若f(1-
3x2)<f(1+x-x2),求x的取值范围.
解 由题意得f(x)的对称轴x=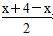 =2,
=2,
∵f(x)的二次项系数为负,
∴f(x)在(-∞,2)上是单调递增,(2,+∞)上单调递减,
又∵1-3x2≤1,1+x-x2≤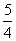 ,
,
∴1-3x2,1+x-x2∈(-∞,2),
又∵f(1-3x2)<f(1+x-x2),∴1-3x2<1+x-x2,
∴x(2x+1)>0,∴x>0或x<-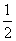
 .
.
∴x的取值范围是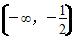 ∪(0,+∞).
∪(0,+∞).

练习册系列答案
相关题目
 b的两个零点是-2和3,则不等式af(-2x)>0的解集是__________.
b的两个零点是-2和3,则不等式af(-2x)>0的解集是__________. _.
_.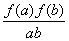
 增函数还是
增函数还是 的单调增区间为________.
的单调增区间为________. ,则
,则 =________.
=________. ,AB=1,BD=PA=2.
,AB=1,BD=PA=2.