题目内容
已知f(x)是定义在[－1,1]上的奇函数，若a、b∈[－1,1]，a＋b≠0时，有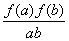
>0.判断函数f(x)在[－1,1]上是
增函数还是减函数，并证明你的结论．
解 f(x)在[－1,1]上是增函数．证明如下：
任取x1、x2∈[－1,1]，且x1<x2，
则－x2∈[－1,1]．又f(x)是奇函数，
则f(x1)－f(x2)＝f(x1)＋f(－x2)＝
(x1－x2)．
据已知
>0，x
1－x2<0，
∴f(x1)－f(x2)<0，即f(x1)<f(x2)．
∴f(x)在[－1,1]上是增函数．
练习册系列答案
全能练考卷系列答案
相关题目
价，以便按新价让利20%销
， 若f(a)>f(－a)，则实数a的取值范围是______________．
(式中字母都是正数)．
在(0，＋∞)上都是减函数，则y＝ax2＋bx在(0，＋∞)上是________
列
函数的定义域：
lg(x－1)＋lg 