题目内容
按如表的规律,2014应当在( )
| 第一列 | 第二列 | 第三列 | 第四列 | 第五列 | |
| 第一行 | 2 | 4 | 6 | 8 | |
| 16 | 14 | 12 | 10 | ||
| 18 | 20 | 22 | 24 | ||
| 32 | 30 | 28 | 26 |
| A、第252行,第2列 |
| B、第252行,第3列 |
| C、第253行,第3列 |
| D、第253行,第4列 |
考点:归纳推理,数列的函数特性
专题:计算题,推理和证明
分析:由题意知,数由偶数构成,且每一行4个数,奇数行从左向右排列,偶数从右向左按大小顺序排列,从而解得.
解答:
解:观察可知,数由偶数构成,
且每一行4个数,
奇数行从左向右排列,
偶数从右向左按大小顺序排列,
而2014÷2=1007,
1007=252×4-1;
故是第252行的数,且是从右向左倒数第二个数,
故在第252行,第2列.
且每一行4个数,
奇数行从左向右排列,
偶数从右向左按大小顺序排列,
而2014÷2=1007,
1007=252×4-1;
故是第252行的数,且是从右向左倒数第二个数,
故在第252行,第2列.
点评:本题考查了归纳推理的应用,属于基础题.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
函数f(x)=ax+loga(x+1)在[0,1]上的最大值与最小值之和为a,则a的值是( )
| A、2 | ||
B、
| ||
| C、4 | ||
D、
|
二次函数f(x)=x2+bx+c在(m,m+1)内有两个不同的实根,则( )
A、f(m)和f(m+1)都大于
| ||
B、f(m)和f(m+1)至少有一个大于
| ||
C、f(m)和f(m+1)都小于
| ||
D、f(m)和f(m+1)至少有一个小于
|
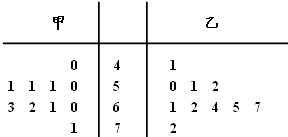 随机抽取某中学甲、乙两班各10名学生,测量他们的体重(单位:kg),获得体重数据的茎叶图如图:
随机抽取某中学甲、乙两班各10名学生,测量他们的体重(单位:kg),获得体重数据的茎叶图如图: