Question

在△ABC中，AD为BC边上的中线，AB=2

5

，BD=2

2

，AD=2，则△ADC的面积S_△ADC=

 

．

Answer 1

考点：正弦定理

专题：解三角形

分析：过A点作AE⊥BC，垂足为点E，由余弦定理可先求AE的值，从而由三角形的面积公式即可△ADC的面积．

解答： 解：过A点作AE⊥BC，垂足为点E，

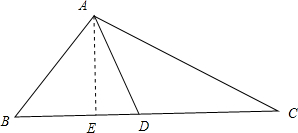
∵AD是BC边上的中线，
∴BD=CD=2

2

，
在△ABD中，AB=2

5

，BD=2

2

，AD=2，
∴cosB=

AB2+BD2-AD2

2•AB×BD

=

3 10

10

，0＜B＜π，
∴sinB=

1-cos2B

=

10

10

，
∴AE=ABsinB=2

5

×

10

10

=

2

∴S_△ADC=S_△ABD=

1

2

AE×DC=

1

2

×

2

×2

2

=2．
故答案为：2．

点评：此题考查了三角形的面积计算，解题的关键是：将△ADC的面积转化为△ABD的面积，属于基本知识的考查．