题目内容
已知曲线C的参数方程为
(θ是参数),P是曲线C与y轴正半轴的交点.以坐标原点O为极点,x轴正半轴为极轴建立极坐标系,求经过点P与曲线C只有一个公共点的直线l的极坐标方程.
|
考点:参数方程化成普通方程,简单曲线的极坐标方程
专题:坐标系和参数方程
分析:利用sin2θ+cos2θ=1把曲线C的参数方程
(θ是参数)化为普通方程,可得圆心与半径,利用圆的切线性质可得直线l的斜率,可得直角坐标方程,再化为极坐标方程即可.
|
解答:
解:利用sin2θ+cos2θ=1把曲线C的参数方程
(θ是参数)化为普通方程得(x-3)2+y2=25.
∴曲线C是圆心为P1(3,0),半径等于5的圆.
∵P是曲线C与y轴正半轴的交点,
∴P(0,4).
根据已知得直线l是圆C经过点P的切线.
∵kPP1=-
,
∴直线l的斜率k=
.
∴直线l的方程为3x-4y+16=0.
∴直线l的极坐标方程为3ρcosθ-4ρsinθ+16=0.
|
∴曲线C是圆心为P1(3,0),半径等于5的圆.
∵P是曲线C与y轴正半轴的交点,
∴P(0,4).
根据已知得直线l是圆C经过点P的切线.
∵kPP1=-
| 4 |
| 3 |
∴直线l的斜率k=
| 3 |
| 4 |
∴直线l的方程为3x-4y+16=0.
∴直线l的极坐标方程为3ρcosθ-4ρsinθ+16=0.
点评:本题考查圆的参数方程和普通方程,考查直线的直角坐标方程和极坐标方程的互化,属于基础题.

练习册系列答案
相关题目
设f(x)是定义在(-∞,+∞)上可导函数且满足xf'(x)+f(x)>0对任意的正数a,b,若a>b则下列不等式恒成立的是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
等差数列{an}的前n项和为Sn,若a2+a7+a12=60,则S13的值是( )
| A、130 | B、260 |
| C、20 | D、150 |
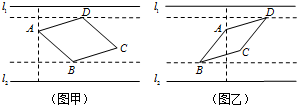 如图,某兴趣小组测得菱形养殖区ABCD的固定投食点A到两条平行河岸线l1、l2的距离分别为4米、8米,河岸线l1与该养殖区的最近点D的距离为1米,l2与该养殖区的最近点B的距离为2米.
如图,某兴趣小组测得菱形养殖区ABCD的固定投食点A到两条平行河岸线l1、l2的距离分别为4米、8米,河岸线l1与该养殖区的最近点D的距离为1米,l2与该养殖区的最近点B的距离为2米.