题目内容
焦点分别为F1,F2的椭圆C:
+
=1(a>b>0)过点M(2,1),且△MF2F1的面积为
,求椭圆C的方程.
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
考点:椭圆的标准方程
专题:计算题,圆锥曲线的定义、性质与方程
分析:利用椭圆C:
+
=1(a>b>0)过点M(2,1),且△MF2F1的面积为
,可得
+
=1,
×2c×1=
,求出a,b,即可求出椭圆C的方程.
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| 4 |
| a2 |
| 1 |
| b2 |
| 1 |
| 2 |
| 3 |
解答:
解:∵椭圆C:
+
=1(a>b>0)过点M(2,1),且△MF2F1的面积为
,
∴
+
=1,
×2c×1=
,
∵a2=b2+c2,
∴c=
,a=
,b=
,
∴椭圆C的方程为
+
=1.
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
∴
| 4 |
| a2 |
| 1 |
| b2 |
| 1 |
| 2 |
| 3 |
∵a2=b2+c2,
∴c=
| 3 |
| 6 |
| 3 |
∴椭圆C的方程为
| x2 |
| 6 |
| y2 |
| 3 |
点评:本题考查椭圆C的方程,考查三角形面积的计算,确定几何量是关键.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
一个人以6米/秒的速度去追赶停在交通灯前的汽车,当他离汽车25米时交通灯由红变绿,汽车开始变速直线行驶(汽车与人前进方向相同),汽车在时间t内的路程为s=
t2米,那么,此人( )
| 1 |
| 2 |
| A、可在7秒内追上汽车 |
| B、可在9秒内追上汽车 |
| C、不能追上汽车,但其间最近距离为14米 |
| D、不能追上汽车,但其间最近距离为7米 |
已知实数x,y满足
则z=2x-y的最小值是( )
|
| A、5 | ||
B、
| ||
| C、-5 | ||
D、-
|
 如图所示,△O′A′B′为斜二测画法做出的△OAB的直观图,其中O′A′=A′B′=2则原△OAB的面积是( )
如图所示,△O′A′B′为斜二测画法做出的△OAB的直观图,其中O′A′=A′B′=2则原△OAB的面积是( )A、2
| ||
| B、4 | ||
C、4
| ||
| D、8 |
已知数列{an}的通项公式an=sin
(n∈N*),则a2014-a2015的值为( )
| nπ |
| 2 |
| A、1 | B、2 | C、-1 | D、0 |
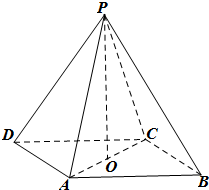 如图,在四棱锥P-ABCD中,底面ABCD为平行四边形,∠DAC=90°,O为AC的中点,PO⊥底面ABCD.
如图,在四棱锥P-ABCD中,底面ABCD为平行四边形,∠DAC=90°,O为AC的中点,PO⊥底面ABCD.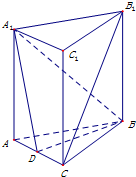 如图,在直三棱柱ABC-A1B1C1中,cos∠A1DD1=
如图,在直三棱柱ABC-A1B1C1中,cos∠A1DD1=