题目内容
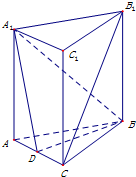 如图,在直三棱柱ABC-A1B1C1中,cos∠A1DD1=
如图,在直三棱柱ABC-A1B1C1中,cos∠A1DD1=| DD1 |
| DA1 |
3
| ||
| 10 |
(Ⅰ)求证:B1C∥平面A1BD;
(Ⅱ)求二面角DO的余弦值.
考点:二面角的平面角及求法,直线与平面平行的判定
专题:空间位置关系与距离,空间角
分析:(Ⅰ)证明线面平行常用以下两种方法:一是用线面平行的判定定理,二是用面面平行的性质.本题用这两种方法都行;
(Ⅱ)首先应考虑作出平面DBB1截三棱柱所得的截面.作出该截面便很容易得到二面角的平面角即为∠A1DD1.本题也可用向量解决.
(Ⅱ)首先应考虑作出平面DBB1截三棱柱所得的截面.作出该截面便很容易得到二面角的平面角即为∠A1DD1.本题也可用向量解决.
解答:
解:(Ⅰ)法一:连结AB1,交A1B于O,连结DO,则B1C∥DO,从而 B1C∥平面A1BD.
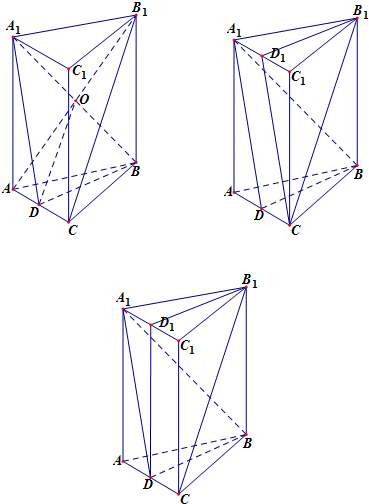
法二:取A1C1的中点D1,连结CD1,易得平面CB1D1∥DBA1,从而 B1C∥平面A1BD.
(Ⅱ)A1C1的中点D1,连结DD1、D1B1,易得平面DBB1D1就是平面DBB1,
又BD⊥平面ACC1A1,所以BD⊥A1D,BD⊥DD1,
所以∠A1DD1就是该二面角的平面角.cos∠A1DD1=
=
.

法二:取A1C1的中点D1,连结CD1,易得平面CB1D1∥DBA1,从而 B1C∥平面A1BD.
(Ⅱ)A1C1的中点D1,连结DD1、D1B1,易得平面DBB1D1就是平面DBB1,
又BD⊥平面ACC1A1,所以BD⊥A1D,BD⊥DD1,
所以∠A1DD1就是该二面角的平面角.cos∠A1DD1=
| DD1 |
| DA1 |
3
| ||
| 10 |
点评:本题考查直线与平面平行的判定定理的应用,二面角的平面角的求法,考查计算能力.

练习册系列答案
相关题目
数列{ncos(nπ)}的前n项和为Sn,(n∈N*),则S2015=( )
| A、2014 | B、2015 |
| C、-1008 | D、-1007 |
圆x2+y2-4x+2y+F=0与y轴交于A,B两点,圆心为C.若∠ACB=90°,则F的值等于( )
A、-2
| ||
B、2
| ||
| C、3 | ||
| D、-3 |
如图表示的算法的输出结果是( )


| A、-2 | ||
B、
| ||
| C、3 | ||
D、
|