题目内容
15．已知双曲线C的右焦点为F，过F的直线l与双曲线C交于不同两点A、B，且A、B两点间的距离恰好等于焦距，若这样的直线l有且仅有两条，则双曲线C的离心率的取值范围为（1，$\frac{1+\sqrt{17}}{4}$）∪（2，+∞）．分析 讨论当A，B均在右支上，可得c＞$\frac{2{b}^{2}}{a}$，当A，B在左右两支上，可得c＞2a，运用离心率公式，解不等式即可得到所求范围．
解答 解：当A，B均在右支上，可得c＞$\frac{2{b}^{2}}{a}$，
即有2b2＜ac，即2c2-ac-2a2＜0，
即为2e2-e-2＜0，
解得1＜e＜$\frac{1+\sqrt{17}}{4}$；
当A，B在左右两支上，可得c＞2a，
即有e＞2．
故答案为：（1，$\frac{1+\sqrt{17}}{4}$）∪（2，+∞）
点评 本题考查双曲线的性质及其应用，解题时要注意挖掘隐含条件，属于中档题
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
5．在某次物理实验中，得到一组不全相等的数据x1，x2，x3，…，xn，若a是这组数据的算术平均数，则a满足（ ）
| A． | $\sum_{i=1}^{n}$（xi-a）最小 | B． | $\sum_{i=1}^{n}$|xi-a|最小 | ||
| C． | $\sum_{i=1}^{n}$（xi-a）2最小 | D． | $\frac{1}{n}$$\sum_{i=1}^{n}$|xi-a|最小 |
6．若数列{an}满足：对任意正整数n，{an+1-an}为递减数列，则称数列{an}为“差递减数列”．给出下列数列{an}（n∈N*）：
①an=3n，②an=n2+1，③an=$\sqrt{n}$，④an=2n-n，⑤an=ln$\frac{n}{n+1}$
其中是“差递减数列”的有（ ）
①an=3n，②an=n2+1，③an=$\sqrt{n}$，④an=2n-n，⑤an=ln$\frac{n}{n+1}$
其中是“差递减数列”的有（ ）
| A． | ③⑤ | B． | ①②④ | C． | ③④⑤ | D． | ②③ |
3．已知双曲线C的中心在坐标原点，F（-2，0）是C的一个焦点，一条渐进线方程为$\sqrt{3}$x-y=0．
（Ⅰ）求双曲线方程；
（Ⅱ）若直线l：y=kx+1与双曲线C有且只有一个公共点，求k的值．
（Ⅰ）求双曲线方程；
（Ⅱ）若直线l：y=kx+1与双曲线C有且只有一个公共点，求k的值．
10．已知抛物线x2=-2y的一条弦AB的中点坐标为（-1，-5），则这条弦AB所在的直线方程是（ ）
| A． | y=x-4 | B． | y=2x-3 | C． | y=-x-6 | D． | y=3x-2 |
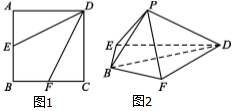如图，在边长为2的正方形ABCD中，点E，F分别是AB，BC的中点，将△AED，△DCF分别沿DE，DF折起，使A，C两点重合于P．