题目内容

计算：
（1）sin
25π
6
+cos
26π
3
+tan（-
25π
4
）；
（2）7log72-（2014）0-(3
3
8
)-
2
3
-log3
427
．
考点：运用诱导公式化简求值
专题：计算题,函数的性质及应用,三角函数的求值
分析：（1）利用三角函数的诱导公式即可求得答案；
（2）利用指数函数与对数函数的运算性质即可求得答案．
解答： 解：（1）原式=sin（4π+
π
6
）+cos（8π+
2π
3
）-tan（6π+
π
4
）
=sin
π
6
+cos
2π
3
-tan
π
4
=
1
2
-
1
2
-1=-1．
（2）原式=2-1-[(
3
2
)3]-
2
3
-
1
4
log3(33)=1-
4
9
-
3
4
=-
7
36
．
点评：本题考查运用三角函数的诱导公式化简求值，考查指数函数与对数函数的运算性质，属于中档题．
练习册系列答案
相关题目
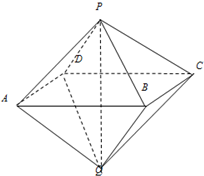如图，已知两个正四棱锥P-ABCD与Q-ABCD的高都是2，AB=4．
（1）求证：PQ⊥平面ABCD；
（2）求点P到平面QAD的距离．
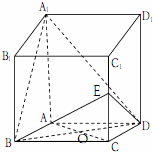四棱柱ABCD-A1B1C1D1中，AA1⊥底面ABCD，且ABCD是菱形，AB=BC=2，AA1=4，∠ABC=60°．
（1）求证：BD⊥平面ACC1A1；
（2）若E是棱CC1的是中点，求二面角A1-BD-E的余弦值．
已知函数f（x）=2
3
sinωxcosωx-2cos2ωx+a（x∈R，ω＞0）的最小正周期为π，最大值为3．
（Ⅰ）求ω和常数a的值；
（Ⅱ）求函数f（x）的单调递增区间．
若二阶矩阵M满足：M
12
34
=
58
46
．
（Ⅰ）求二阶矩阵M；
（Ⅱ）若曲线C：x2+2xy+2y2=1在矩阵M所对应的变换作用下得到曲线C′，求曲线C′的方程．
（理）设F1，F2分别为椭圆W：
x2
6
+
y2
2
=1的左、右焦点，斜率为k（k＞0）直线L经过右焦点F2，且与椭圆W相交于A，B两点．
（1）如果线段F2B的中点在y轴上，求直线l的方程；
（2）如果△ABF1为直角三角形，求直线l的斜率k．
已知函数f（x）=
1
ax+2
（x∈R，a为常数），P1（x1，y1），P2（x2，y2）是函数y=f（x）图象上的两点．当线段P1P2的中点P的横坐标为
1
2
时，P的纵坐标恒为
1
4
．
（1）求y=f（x）的解析式；
（2）若数列{an}的通项公式为an=f（
n
n0
）（n0∈N*，n=1，2，…，n），求数列{an}的前n0和Sn0．
设函数f（x）是定义在R上的奇函数，且对任意实数x，都有f（x+2）=-f（x），当x∈[0，2]时，f（x）=2x-x2．
（1）求证：f（x）是周期函数，并求出最小正周期；
（2）当x∈[2，4]时，求f（x）解析式；
（3）求f（0）+f（1）+f（2）+…+f（2012）值．
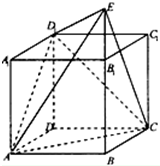如图，直四棱柱ABCD-A1B1C1D1中，底面ABCD为菱形，且∠BAD=60°，A1A=AB，E为BB1延长线上的一点，D1E⊥面D1AC，设AB=2．
（1）求二面角E-AC-D1的余弦值；
（2）在D1E上是否存在一点P，使A1P∥面EAC？若存在，求D1P：PE的值；若不存在，请说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网