题目内容
已知函数f(x)=2
sinωxcosωx-2cos2ωx+a(x∈R,ω>0)的最小正周期为π,最大值为3.
(Ⅰ)求ω和常数a的值;
(Ⅱ)求函数f(x)的单调递增区间.
| 3 |
(Ⅰ)求ω和常数a的值;
(Ⅱ)求函数f(x)的单调递增区间.
考点:三角函数中的恒等变换应用,正弦函数的图象
专题:三角函数的图像与性质
分析:(Ⅰ)利用三角恒等变换,可求得f(x)=2sin(2ωx-
)+a-1,依题意,可得ω和常数a的值;
(Ⅱ)由(Ⅰ)知,f(x)=2sin(2x-
)+1,利用正弦函数的单调性质即可求得函数f(x)的单调递增区间.
| π |
| 6 |
(Ⅱ)由(Ⅰ)知,f(x)=2sin(2x-
| π |
| 6 |
解答:
解:(Ⅰ)f(x)=2
sinωxcosωx-2cos2ωx+a
=
sin2ωx-cos2ωx+a-1
=2(
sin2ωx-
cos2ωx)+a-1
=2sin(2ωx-
)+a-1,
∵f(x)的最小正周期为π,最大值为3,
∴
=π,ω=1;a+1=3,a=2;
(Ⅱ)由(Ⅰ)知,f(x)=2sin(2x-
)+1,
由-
+2kπ≤2x-
≤
+2kπ,k∈Z得:kπ-
≤x≤
+kπ,k∈Z.
∴函数f(x)的单调递增区间为[kπ-
,
+kπ],k∈Z.
| 3 |
=
| 3 |
=2(
| ||
| 2 |
| 1 |
| 2 |
=2sin(2ωx-
| π |
| 6 |
∵f(x)的最小正周期为π,最大值为3,
∴
| 2π |
| 2ω |
(Ⅱ)由(Ⅰ)知,f(x)=2sin(2x-
| π |
| 6 |
由-
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
| π |
| 6 |
| π |
| 3 |
∴函数f(x)的单调递增区间为[kπ-
| π |
| 6 |
| π |
| 3 |
点评:本题考查三角函数中的恒等变换应用,求得f(x)=2sin(2ωx-
)+a-1是关键,考查正弦函数的周期性、单调性及最值的应用,属于中档题.
| π |
| 6 |

练习册系列答案
相关题目
若A={x|-1<x<2},B={x|1<x<3},则A∩B=( )
| A、{x|1<x<2} |
| B、{x|-1<x<3} |
| C、{x|1<x<3} |
| D、{x|-1<x<2} |
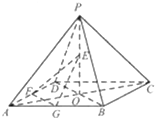 如图,四棱锤P-ABCD的底面为正方形,每题侧棱的长都等于底面的长,AC∩BD=O,E、F、G分别是PO、AD、AB的中点.
如图,四棱锤P-ABCD的底面为正方形,每题侧棱的长都等于底面的长,AC∩BD=O,E、F、G分别是PO、AD、AB的中点.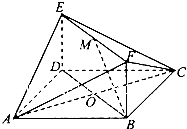 如图,已知正方形ABCD和矩形BDFE所在的平面互相垂直,AC交BD于O点,M为EF的中点,BC=
如图,已知正方形ABCD和矩形BDFE所在的平面互相垂直,AC交BD于O点,M为EF的中点,BC=