题目内容
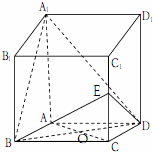 四棱柱ABCD-A1B1C1D1中,AA1⊥底面ABCD,且ABCD是菱形,AB=BC=2,AA1=4,∠ABC=60°.
四棱柱ABCD-A1B1C1D1中,AA1⊥底面ABCD,且ABCD是菱形,AB=BC=2,AA1=4,∠ABC=60°.(1)求证:BD⊥平面ACC1A1;
(2)若E是棱CC1的是中点,求二面角A1-BD-E的余弦值.
考点:与二面角有关的立体几何综合题,直线与平面平行的判定
专题:空间位置关系与距离,空间角
分析:(1)由线面垂直得AA1⊥BD,由菱形性质得AC⊥BD,由此能证明BD⊥平面ACC1A1.
(2)连结A1O,EO,A1E,由已知条件推导出∠A1OE是二面角A1-BD-E的平面角,由此能求出二面角A1-BD-E的平面角的余弦值.
(2)连结A1O,EO,A1E,由已知条件推导出∠A1OE是二面角A1-BD-E的平面角,由此能求出二面角A1-BD-E的平面角的余弦值.
解答:
(1)证明:在四棱柱ABCD-A1B1C1D1中,
∵AA1⊥平面ABCD,∴AA1⊥BD,
∵平行四边形ABCD中,AB=BC,
∴AC⊥BD,
∵AA1∩AC=A,
∴BD⊥平面ACC1A1.
(2)解:连结A1O,EO,A1E,
∵在四棱柱中,底面ABCD是棱形,且E是棱CC1的中点,
∴A1B=A1D,EB=ED,又∵O是BD的中点,
∴A1B=A1D,EB=ED,
又∵O是BD的中点,∴A1O⊥BD,EO⊥BD,
∴∠A1OE是二面角A1-BD-E的平面角,
∵四棱柱中,AA1⊥平面ABCD,AB=BC=2,AA1=4,
∴A1O=
,EO=
,A1E=2
,
∴在△A1OE中,cos∠A1OE=
=
=
,
∴二面角A1-BD-E的平面角的余弦值为
.
∵AA1⊥平面ABCD,∴AA1⊥BD,

∵平行四边形ABCD中,AB=BC,
∴AC⊥BD,
∵AA1∩AC=A,
∴BD⊥平面ACC1A1.
(2)解:连结A1O,EO,A1E,
∵在四棱柱中,底面ABCD是棱形,且E是棱CC1的中点,
∴A1B=A1D,EB=ED,又∵O是BD的中点,
∴A1B=A1D,EB=ED,
又∵O是BD的中点,∴A1O⊥BD,EO⊥BD,
∴∠A1OE是二面角A1-BD-E的平面角,
∵四棱柱中,AA1⊥平面ABCD,AB=BC=2,AA1=4,
∴A1O=
| 17 |
| 5 |
| 2 |
∴在△A1OE中,cos∠A1OE=
| A1O2+EO2-A1E2 |
| 2A1O•EO |
| 17+5-8 | ||||
2
|
7
| ||
| 85 |
∴二面角A1-BD-E的平面角的余弦值为
7
| ||
| 85 |
点评:本题考查直线与平面垂直的证明,考查二面角的余弦值的求法,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
数列1,
,
,
,
,
,…,
,
,…,
…的前18项的和( )
| 1 |
| 2 |
| 2 |
| 2 |
| 1 |
| 3 |
| 2 |
| 3 |
| 3 |
| 3 |
| 1 |
| n |
| 2 |
| n |
| n |
| n |
| A、11 | ||
B、
| ||
C、
| ||
| D、10 |
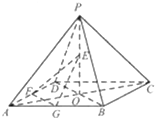 如图,四棱锤P-ABCD的底面为正方形,每题侧棱的长都等于底面的长,AC∩BD=O,E、F、G分别是PO、AD、AB的中点.
如图,四棱锤P-ABCD的底面为正方形,每题侧棱的长都等于底面的长,AC∩BD=O,E、F、G分别是PO、AD、AB的中点.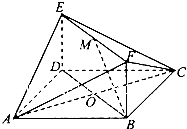 如图,已知正方形ABCD和矩形BDFE所在的平面互相垂直,AC交BD于O点,M为EF的中点,BC=
如图,已知正方形ABCD和矩形BDFE所在的平面互相垂直,AC交BD于O点,M为EF的中点,BC=