题目内容
若二阶矩阵M满足:M
=
.
(Ⅰ)求二阶矩阵M;
(Ⅱ)若曲线C:x2+2xy+2y2=1在矩阵M所对应的变换作用下得到曲线C′,求曲线C′的方程.
|
|
(Ⅰ)求二阶矩阵M;
(Ⅱ)若曲线C:x2+2xy+2y2=1在矩阵M所对应的变换作用下得到曲线C′,求曲线C′的方程.
考点:矩阵与向量乘法的意义,变换、矩阵的相等
专题:选作题,矩阵和变换
分析:(Ⅰ)先求矩阵的逆矩阵,即可求二阶矩阵M;
(Ⅱ)设二阶矩阵M所对应的变换,根据矩阵变换求出坐标之间的关系,代入已知曲线求出所求曲线即可.
(Ⅱ)设二阶矩阵M所对应的变换,根据矩阵变换求出坐标之间的关系,代入已知曲线求出所求曲线即可.
解答:
解:(Ⅰ)设A=
,则|A|=
=-2,∴A-1=
,…(2分)
∴M=
=
. …(3分)
(Ⅱ)∵M
=
∴
=M-1
=
,
即
…(4分)
代入x2+2xy+2y2=1可得(x'-y')2+2(x'-y')(-x'+2y')+2(-x'+2y')2=1,即x'2-4x'y'+5y'2=1,
故曲线C'的方程为x2-4xy+5y2=1. …(7分)
|
|
|
∴M=
|
|
|
(Ⅱ)∵M
|
|
|
|
|
|
即
|
代入x2+2xy+2y2=1可得(x'-y')2+2(x'-y')(-x'+2y')+2(-x'+2y')2=1,即x'2-4x'y'+5y'2=1,
故曲线C'的方程为x2-4xy+5y2=1. …(7分)
点评:本题主要考查来了逆矩阵与矩阵变换的性质,熟练掌握矩阵的运算法则是解答的关键,属于基础题.

练习册系列答案
相关题目
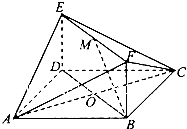 如图,已知正方形ABCD和矩形BDFE所在的平面互相垂直,AC交BD于O点,M为EF的中点,BC=
如图,已知正方形ABCD和矩形BDFE所在的平面互相垂直,AC交BD于O点,M为EF的中点,BC=