题目内容
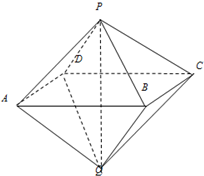 如图,已知两个正四棱锥P-ABCD与Q-ABCD的高都是2,AB=4.
如图,已知两个正四棱锥P-ABCD与Q-ABCD的高都是2,AB=4. (1)求证:PQ⊥平面ABCD;
(2)求点P到平面QAD的距离.
考点:点、线、面间的距离计算,直线与平面垂直的判定
专题:综合题,空间位置关系与距离
分析:(1)取AD的中点M,连结PM,QM,证明PQ⊥AD,PQ⊥AB,即可证明PQ⊥平面ABCD;
(2)证明PM⊥平面QAD,可得PM的长是点P到平面QAD的距离,即可求点P到平面QAD的距离.
(2)证明PM⊥平面QAD,可得PM的长是点P到平面QAD的距离,即可求点P到平面QAD的距离.
解答:
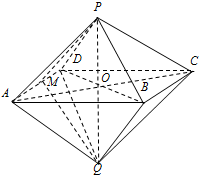 (1)证明:取AD的中点M,连结PM,QM.
(1)证明:取AD的中点M,连结PM,QM.
因为P-ABCD与Q-ABCD都是正四棱锥,
所以AD⊥PM,AD⊥QM,从而AD⊥平面PQM.
又PQ?平面PQM,所以PQ⊥AD.
同理PQ⊥AB.
又AD?平面ABCD,AB?平面ABCD,AD∩AB=A,所以PQ⊥平面ABCD.
(2)解:连结OM,则OM=
AB=2=
PQ.
所以∠PMQ=90°,即PM⊥MQ.
由(1)知AD⊥PM,所以PM⊥平面QAD.
所以PM的长是点P到平面QAD的距离.
在Rt△PMO中,PM=
=
=2
.
所以点P到平面QAD的距离为2
.
 (1)证明:取AD的中点M,连结PM,QM.
(1)证明:取AD的中点M,连结PM,QM.因为P-ABCD与Q-ABCD都是正四棱锥,
所以AD⊥PM,AD⊥QM,从而AD⊥平面PQM.
又PQ?平面PQM,所以PQ⊥AD.
同理PQ⊥AB.
又AD?平面ABCD,AB?平面ABCD,AD∩AB=A,所以PQ⊥平面ABCD.
(2)解:连结OM,则OM=
| 1 |
| 2 |
| 1 |
| 2 |
所以∠PMQ=90°,即PM⊥MQ.
由(1)知AD⊥PM,所以PM⊥平面QAD.
所以PM的长是点P到平面QAD的距离.
在Rt△PMO中,PM=
| PO2+OM2 |
| 22+22 |
| 2 |
所以点P到平面QAD的距离为2
| 2 |
点评:本题考查线面垂直,考查点到平面距离的计算,考查学生分析解决问题的能力,确定PM的长是点P到平面QAD的距离是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知f(x)=
,则f(5)=( )
| x+2 |
| x-6 |
| A、-8 | B、-7 | C、-6 | D、-5 |
数列1,
,
,
,
,
,…,
,
,…,
…的前18项的和( )
| 1 |
| 2 |
| 2 |
| 2 |
| 1 |
| 3 |
| 2 |
| 3 |
| 3 |
| 3 |
| 1 |
| n |
| 2 |
| n |
| n |
| n |
| A、11 | ||
B、
| ||
C、
| ||
| D、10 |
若A={x|-1<x<2},B={x|1<x<3},则A∩B=( )
| A、{x|1<x<2} |
| B、{x|-1<x<3} |
| C、{x|1<x<3} |
| D、{x|-1<x<2} |